题目内容
【题目】如图,在![]() 中,
中,![]() .点
.点![]() 为
为![]() 的中点,点
的中点,点![]() 为射线
为射线![]() 上一点,将
上一点,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,设
,设![]() ,
,![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,
,![]() 关于
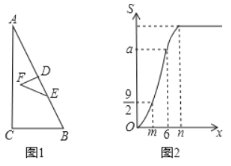
关于![]() 的函数图象如图2所示(其中
的函数图象如图2所示(其中![]() ,
,![]() ,
,![]() ,
,![]() 时,函数的解析式不同).则
时,函数的解析式不同).则![]() __.
__.
【答案】![]()
【解析】
当点F在AC上时,先求此时DF=3,由已知的图2知:当x=m=3时,S=![]() ,即当0<x≤3时,点F在AC上时,S最大,在这一取值重叠部分是△EDF,图2中最后一个阶段:计算当EF过点C时,所对应的DE的长,就是n的值,作辅助线,构建等腰直角三角形CHE,先根据面积法求高线CH的长,再分别求DH和EH的长,可得x的值,即n的值.
,即当0<x≤3时,点F在AC上时,S最大,在这一取值重叠部分是△EDF,图2中最后一个阶段:计算当EF过点C时,所对应的DE的长,就是n的值,作辅助线,构建等腰直角三角形CHE,先根据面积法求高线CH的长,再分别求DH和EH的长,可得x的值,即n的值.
解:(1)∵DE=x,
由旋转可得:△DEF是等腰三角形,
∴![]()
由已知图2得:![]() ,
,
解得:![]()
∵m>0,
∴m=3,
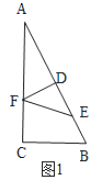
当点F在AC上时,如图1,DE=DF=3,
∵BD=6,即当x=6时,点E与B重合,如图2,

此时,DG=3,GF=6-3=3,
∵D是AB的中点,
∴AD=BD=6,
tan∠DGA=tan∠MGH=![]()
∴MH=2MG,
∵∠F=45°,
∴△MHF是等腰直角三角形,
∴FM=MH=2MG,
∵FG=3,
∴FM=MH=2,
∴![]()
∴a=15,
当EF经过点C时,如图3,过C作CH⊥AB于H,

![]()
∵AB=12,
∴![]()
∴![]() ,即
,即![]() ,
,![]()
∵∠AEC=45°,
∴△CHE是等腰直角三角形,
∴![]()
∴![]()
∴![]()
故答案为:![]()

【题目】某商场用36万元购进A、B两种商品,销售完后共获利6万元,其进价和售价如下表:
A | B | |
进价(元/件) | 1200 | 1000 |
售价(元/件) | 1380 | 1200 |
(注:获利=售价-进价)
(1) 该商场购进A、B两种商品各多少件?
(2) 商场第二次以原进价购进A、B两种商品.购进B种商品的件数不变,而购进A种商品的件数是第一次的2倍,A种商品按原价出售,而B种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于81600元,B种商品最低售价为每件多少元?