题目内容
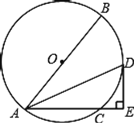
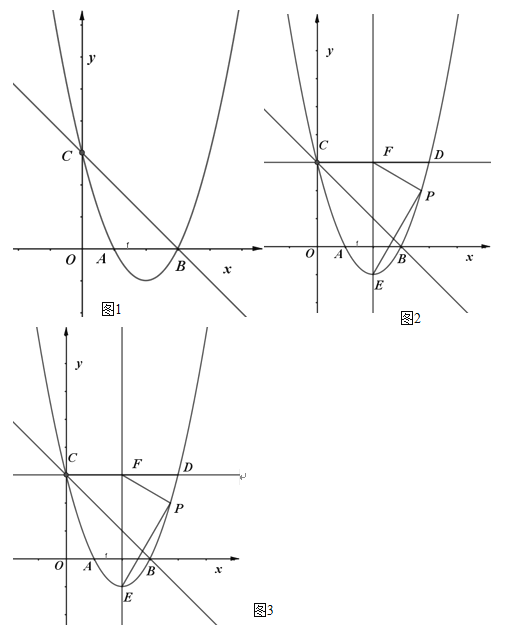
【题目】如图1,![]() 是
是![]() 的内角,
的内角,![]() ,
,

(1)![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,过点
,过点![]() 作
作![]() ,判断四边形
,判断四边形![]() 的形状:________;
的形状:________;
(2)旋转![]() 到
到![]() ,如图2,边
,如图2,边![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,AE=AF.过点
,AE=AF.过点![]() 作
作![]() ,过点
,过点![]() 作
作![]() .问:
.问:![]() 是否平分
是否平分![]() .若是请证明,若不是请说明理由.
.若是请证明,若不是请说明理由.
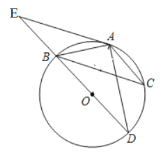
(3)四边形![]() 在(2)的条件下,若恰好
在(2)的条件下,若恰好![]() ,如图3.连接
,如图3.连接![]() 并延长,交
并延长,交![]() 的延长线于点
的延长线于点![]() .求证:
.求证:![]() .
.
【答案】(1)菱形;(2)![]() 平分
平分![]() ;理由见解析;(3)证明见解析
;理由见解析;(3)证明见解析
【解析】
(1)根据平行四边形的定义可得四边形ABFG为平行四边形,然后证出△FAB为等边三角形可得BF=BA,从而得出结论;
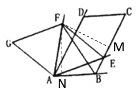
(2)过点![]() 作
作![]() 于N,作
于N,作![]() 于M,先证出
于M,先证出![]() 是等边三角形,然后利用SAS证出
是等边三角形,然后利用SAS证出![]() ,从而得出
,从而得出![]() ,然后根据角平分线的判定即可证出结论;
,然后根据角平分线的判定即可证出结论;
(3)先证出平行四边形![]() 是菱形,从而得出
是菱形,从而得出![]() ,然后设
,然后设![]() 、
、![]() 交于点
交于点![]() ,根据30°所对的直角边是斜边的一半即可得出
,根据30°所对的直角边是斜边的一半即可得出![]() ,然后结合平行四边形的性质和等角对等边即可证出结论.
,然后结合平行四边形的性质和等角对等边即可证出结论.
解:(1)∵![]() ,
,![]()
∴四边形ABFG为平行四边形
∵![]() 中,
中,![]()
∴∠ABC=180°-∠DAB=120°
∵![]() 平分
平分![]() ,
,
∴∠ABF=![]() =60°
=60°
∴∠AFB=180°-∠ABF-∠FAB=60°
∴△FAB为等边三角形
∴BF=BA
∴四边形ABFG为菱形
故答案为:菱形;
(2)答:![]() 平分
平分![]()
理由:过点![]() 作
作![]() 于N,作
于N,作![]() 于M
于M
∴![]()
∵由题意得:![]() , AE=AF
, AE=AF
∴![]() 是等边三角形
是等边三角形
∴![]()
∴![]()
∵![]()
即:![]()
∵在![]() 中,
中,![]() ,
,
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
又∵![]() ,作
,作![]()
∴![]() 平分
平分![]()
(3)∵![]() ,
,![]()
∴四边形![]() 是平行四边形
是平行四边形
∵由(2)知![]()
∴平行四边形![]() 是菱形
是菱形
∴![]()
∵![]()
∴![]()
∵![]()
∴![]() ,
,
∴![]() ,
,![]()
设![]() 、
、![]() 交于点
交于点![]()
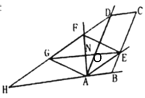
在![]() 中,
中,![]()
∵![]() ,
,![]()
∴四边形![]() 为平行四边形
为平行四边形
∴![]()
∵![]() ,
,
∵四边形![]() 为平行四边形
为平行四边形
∴![]() ,
,![]()
∴四边形![]() 为平行四边形,
为平行四边形,
又∵![]()
∴![]()
∴![]()
∵![]() ,
,![]()
∴![]() ,
,
∵![]()
∴![]()
∴![]()
∴![]()

练习册系列答案
相关题目