题目内容
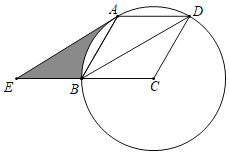
【题目】如图⑴,在△ABC中,∠C=90°,AC=8cm,BC=6cm. 点M由点B出发沿BA方向向点A匀速运动,同时点N由点A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s .连接MN,设运动时间为t(s)﹙0<t<4﹚,解答下列问题:
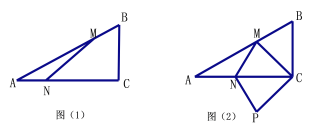
⑴设△AMN的面积为S,求S与t之间的函数关系式,并求出S的最大值;
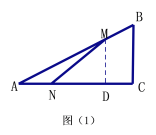
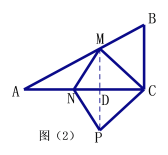
⑵如图⑵,连接MC,将△MNC沿NC翻折,得到四边形MNPC,当四边形MNPC为菱形时,求t的值;
⑶当t的值为 ,△AMN是等腰三角形.
【答案】(1)![]() ,
, ![]() ;(2)t=
;(2)t=![]() ;(3)
;(3)![]() 或
或![]() 或
或![]()
【解析】
(1)如图过点M作MD⊥AC于点D,利用相似三角形的性质求出MD即可解决问题;
(2)连接PM,交AC于D,,当四边形MNPC为菱形时,ND=![]() ,即可用t表示AD,再结合第一问的相似可以用另外一个含t式子表示AD,列方程计算即可;
,即可用t表示AD,再结合第一问的相似可以用另外一个含t式子表示AD,列方程计算即可;
(3)分别用t表示出AP、AQ、PQ,再分三种情况讨论:①当AQ=AP②当PQ=AQ③当PQ=AP,再分别计算即可.
解:⑴过点M作MD⊥AC于点D.
∵![]() ,
,![]() ;
;
∴AB=10cm.BM=AN=2t
∴AM=10-2t.
∵△ADM∽△ACB
∴![]() 即
即![]()
∴![]()
∴![]()
又![]()
∴S的最大值是![]() ;
;
⑵连接PM,交AC于D,
∵四边形MNPC是菱形,则MP⊥NC,ND=CD
∵CN=8-2t
∴ND=4-t
∴AD=2t+4-t=t+4
由⑴知AD=![]()
∴![]() =t+4
=t+4
∴t=![]() ;
;
(3)由(1)知,PE=﹣![]() t+3,与(2)同理得:QE=AE﹣AQ=﹣
t+3,与(2)同理得:QE=AE﹣AQ=﹣![]() t+4
t+4
∴PQ=![]() =
=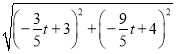 =
=![]() ,
,
在△APQ中,
①当AQ=AP,即t=5﹣t时,解得:t1=![]() ;
;
②当PQ=AQ,即![]() =t时,解得:t2=
=t时,解得:t2=![]() ,t3=5;
,t3=5;
③当PQ=AP,即![]() =5﹣t时,解得:t4=0,t5=
=5﹣t时,解得:t4=0,t5=![]() ;
;
∵0<t<4,
∴t3=5,t4=0不合题意,舍去,
∴当t为![]() s或
s或![]() s或
s或![]() s时,△APQ是等腰三角形.
s时,△APQ是等腰三角形.

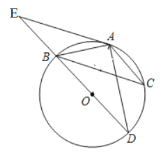
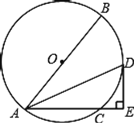
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)如果∠BAC=60°,AE=![]() ,求AC长.
,求AC长.
【题目】![]() 城有肥料
城有肥料![]() ,
,![]() 城有肥料
城有肥料![]() .现要把这些肥料全部运往
.现要把这些肥料全部运往![]() 、
、![]() 两乡,
两乡,![]() 乡需要肥料240t,
乡需要肥料240t,![]() 乡需要肥料
乡需要肥料![]() ,其运往
,其运往![]() 、
、![]() 两乡的运费如下表:
两乡的运费如下表:
两城/两乡 | C/(元/ | D/(元/ |
| 20 | 24 |
| 15 | 17 |
设从![]() 城运往
城运往![]() 乡的肥料为
乡的肥料为![]() ,从
,从![]() 城运往两乡的总运费为
城运往两乡的总运费为![]() 元,从
元,从![]() 城运往两乡的总运费为
城运往两乡的总运费为![]() 元
元
(1)分别写出![]() 、
、![]() 与
与![]() 之间的函数关系式(不要求写自变量的取值范围);
之间的函数关系式(不要求写自变量的取值范围);
(2)试比较![]() 、
、![]() 两城总运费的大小;
两城总运费的大小;
(3)若![]() 城的总运费不得超过4800元,怎样调运使两城总费用的和最少?并求出最小值.
城的总运费不得超过4800元,怎样调运使两城总费用的和最少?并求出最小值.