题目内容
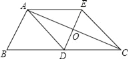
【题目】如图.在△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作与DE∥AB,DE与AC、AE分别交于点O、E,连接EC.
(1)求证:AD=EC;
(2)当△ABC满足 时,四边形ADCE是菱形.
【答案】(1)见解析;(2)∠BAC=90°.
【解析】
(1)首先证明四边形ABDE是平行四边形,可得AE=BD,再根据DC=DB可得AE=DC,进而证出四边形ADCE是平行四边形,可得AD=EC;(2)当∠BAC=90°时,可证出AD=DC,再根据有一组邻边相等的平行四边形是菱形可得四边形ADCE是菱形.
证明:(1)∵DE∥AB,AE∥BC,
∴四边形ABDE是平行四边形,
∴AE∥BD,且AE=BD
又∵AD是BC边的中线,
∴BD=CD,
∴AE=CD,
∵AE∥CD,
∴四边形ADCE是平行四边形,
∴AD=EC;
(2)∵∠BAC=90°,AD是斜边BC上的中线,
∴AD=BD=CD,
又∵四边形ADCE是平行四边形,
∴四边形ADCE是菱形.
故答案为∠BAC=90°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某校为了从甲、乙两名学生中选派一名学生参加市综合知识技能竞赛,对他们进 行了 8 次综合知识技能测试,记录如下:
学生 | 8 次测试成绩(分) | 平均数 | 中位数 | 方差 | |||||||
甲 | 95 | 82 | 88 | 81 | 93 | 79 | 84 | 78 | 85 | 35.5 | |
乙 | 83 | 92 | 80 | 95 | 90 | 80 | 85 | 75 | 84 | ||
(1)请你通过计算求出表格中所缺少的甲、乙两名学生这 8 次测试成绩的平均数、中位数 和方差;
(2)现要从中选派一人参加市综合知识技能竞赛,你认为选派哪名同学参加合适,请说明 理由.