题目内容
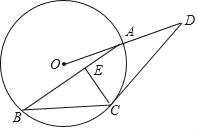
【题目】如图,已知点A,B,C在半径为4的⊙O上,过点C作⊙O的切线交OA的延长线于点D.
(Ⅰ)若∠ABC=29°,求∠D的大小;
(Ⅱ)若∠D=30°,∠BAO=15°,作CE⊥AB于点E,求:
①BE的长;
②四边形ABCD的面积.
【答案】(1)∠D=32°;(2)①BE=![]() ;②
;②![]()
【解析】
(Ⅰ)连接OC, CD为切线,根据切线的性质可得∠OCD=90°,根据圆周角定理可得∠AOC=2∠ABC=29°×2=58°,根据直角三角形的性质可得∠D的大小.
(Ⅱ)①根据∠D=30°,得到∠DOC=60°,根据∠BAO=15°,可以得出∠AOB=150°,进而证明△OBC为等腰直角三角形,根据等腰直角三角形的性质得出![]()
根据圆周角定理得出![]() 根据含
根据含![]() 角的直角三角形的性质即可求出BE的长;
角的直角三角形的性质即可求出BE的长;
②根据四边形ABCD的面积=S△OBC+S△OCD﹣S△OAB进行计算即可.
(Ⅰ)连接OC,
∵CD为切线,
∴OC⊥CD,
∴∠OCD=90°,
∵∠AOC=2∠ABC=29°×2=58°,
∴∠D=90°﹣58°=32°;
(Ⅱ)①连接OB,
在Rt△OCD中,∵∠D=30°,
∴∠DOC=60°,![]()
∵∠BAO=15°,
∴∠OBA=15°,
∴∠AOB=150°,
∴∠OBC=150°﹣60°=90°,
∴△OBC为等腰直角三角形,
∴![]()
∵![]()
在Rt△CBE中,![]()
∴![]()
②作BH⊥OA于H,如图,
∵∠BOH=180°﹣∠AOB=30°,
∴![]()
∴四边形ABCD的面积=S△OBC+S△OCD﹣S△OAB
![]()

练习册系列答案
相关题目