题目内容
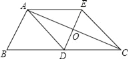
【题目】如图,把长方形纸片![]() 沿
沿![]() 折叠后,使得点
折叠后,使得点![]() 与点
与点![]() 重合,点
重合,点![]() 落在点
落在点![]() 的位置上.
的位置上.

(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)求证:![]() ;
;
(3)若![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() ;(2)证明见解析;(3)22. 5
;(2)证明见解析;(3)22. 5
【解析】
(1)根据矩形的性质和平行线的性质可得∠2=∠1=60°,然后根据折叠的性质可得∠BEF=∠2=60°,从而求出∠3的度数;
(2)根据矩形的性质和平行线的性质可得∠2=∠1,然后根据折叠的性质可得∠BEF=∠2,从而证出:∠BEF=∠1,最后根据等角对等边即可证出![]() ;
;
(3)过点E作EG⊥BC于G,根据平行线之间的距离处处相等即可求出:EG=AB=6,由折叠的性质,可设BE=ED=x,则AE=12-x,然后根据勾股定理列出方程,即可求出x的值,根据(2)的结论即可求出BF从而求出![]() 的面积.
的面积.
解:(1)∵四边形ABCD是长方形
∴AD∥BC
∴∠2=∠1=60°
由折叠可知:∠BEF=∠2=60°
∴∠3=180°-∠BEF-∠2=60°
(2)∵四边形ABCD是长方形
∴AD∥BC
∴∠2=∠1
由折叠可知:∠BEF=∠2
∴∠BEF=∠1
∴![]()
(3)过点E作EG⊥BC于G,如下图所示,
∴EG=AB=6
由折叠的性质,可设BE=ED=x,则AE=12-x
根据勾股定理:![]()
∴![]()
解得:x=7.5
∴![]()
∴![]()

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案【题目】如图,A、B、C是三个垃圾存放点,点B、C分别位于点A的正北和正东方向,AC=200米,编号为1﹣6号的6名同学分别测得∠C的度数如下表:
1号 | 2号 | 3号 | 4号 | 5号 | 6号 | |
∠C(单位:度) | 37 | 36 | 37 | 40 | 34 | 38 |
他们又调查了各点的垃圾量,并绘制了下列尚不完整的统计图,如图:
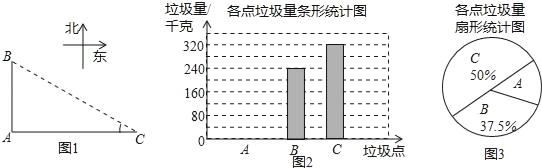
(1)求表中∠C度数的平均数,众数和中位数;
(2)求A处的垃圾量,并将图2补充完整;
(3)用(1)中的![]() 作为∠C的度数,要将A处的垃圾沿道路AB都运到B处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用:(注:sin37°=0.6,cos37°=0.8,tan37°=0.75)
作为∠C的度数,要将A处的垃圾沿道路AB都运到B处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用:(注:sin37°=0.6,cos37°=0.8,tan37°=0.75)