题目内容
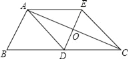
【题目】如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下三个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°.其中结论正确的结论是()

A.①②③B.①②C.①③D.②③
【答案】A
【解析】
①由AB=AC,AD=AE,利用等式的性质得到夹角相等,利用SAS得出三角形ABD与三角形AEC全等,由全等三角形的对应边相等得到BD=CE,本选项正确;
②由三角形ABD与三角形AEC全等,得到一对角相等,再利用等腰直角三角形的性质及等量代换得到BD垂直于CE,本选项正确;
③由等腰直角三角形的性质得到∠ABD+∠DBC=45°,等量代换得到∠ACE+∠DBC=45°,本选项正确.
解:①∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,
∵在△BAD和△CAE中, ,
,
∴△BAD≌△CAE(SAS),
∴BD=CE,
∴选项①正确;
②∵△BAD≌△CAE,
∴∠ABD=∠ACE,
∵∠ABD+∠DBC=45°,
∴∠ACE+∠DBC=45°,
∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°,
∴BD⊥CE,
∴选项②正确;
③∵△ABC为等腰直角三角形,
∴∠ABC=∠ACB=45°,
∴∠ABD+∠DBC=45°,
∵∠ABD=∠ACE
∴∠ACE+∠DBC=45°,
∴选项③正确;
综上所述,正确的结论有①②③.
故选:A.

 天天练口算系列答案
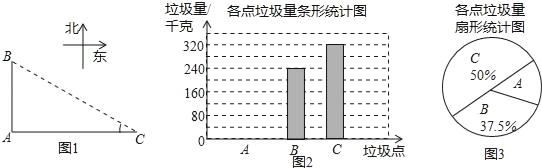
天天练口算系列答案【题目】如图,A、B、C是三个垃圾存放点,点B、C分别位于点A的正北和正东方向,AC=200米,编号为1﹣6号的6名同学分别测得∠C的度数如下表:
1号 | 2号 | 3号 | 4号 | 5号 | 6号 | |
∠C(单位:度) | 37 | 36 | 37 | 40 | 34 | 38 |
他们又调查了各点的垃圾量,并绘制了下列尚不完整的统计图,如图:
(1)求表中∠C度数的平均数,众数和中位数;
(2)求A处的垃圾量,并将图2补充完整;
(3)用(1)中的![]() 作为∠C的度数,要将A处的垃圾沿道路AB都运到B处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用:(注:sin37°=0.6,cos37°=0.8,tan37°=0.75)
作为∠C的度数,要将A处的垃圾沿道路AB都运到B处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用:(注:sin37°=0.6,cos37°=0.8,tan37°=0.75)