题目内容
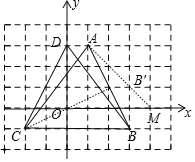
【题目】已知点A(1,3)、B(3,-1),利用图中的“格点”完成下列作图并解答:

(1)在第三象限内找“格点”C,使得CA=CB,则点C的坐标是 ;
(2)在(1)的基础上,标出“格点”D,使得△DCB≌△ABC,则点D的坐标是 ;
(3)点M是x轴上一点,且MA-MB的值最大,则点M的坐标是 .
【答案】(1)(-2,-1);(2)(0,3);(3)(4,0).
【解析】
(1)点C在线段AB的垂直平分线上;(2)根据全等三角形的性质即可解决问题;(3)作点B关于x轴的对称点B′,连接AB′,延长AB′交x轴于点M,点M即为所求,M(4,0).
解:(1)∵CA=CB
∴点C在线段AB的垂直平分线上
∴格点C(-2,-1)如图所示.
(2)利用“SSS”定理作图确定,格点D(0,3)如图所示.
(3)作点B关于x轴的对称点B′,连接AB′,延长AB′交x轴于点M,点M即为所求,M(4,0).

练习册系列答案
相关题目
【题目】为了争创全国文明卫生城市,优化城市环境,某市公交公司决定购买一批共10台全新的混合动力公交车,现有A、B两种型号,其中每台的价格,年省油量如下表:
A | B | |
价格(万元/台) | a | b |
节省的油量(万升/年) | 2.4 | 2 |
经调查,购买一台A型车比购买一台B型车多20万元,购买2台A型车比购买3台B型车少60万元.
(1)请求出a和b;
(2)若购买这批混合动力公交车(两种车型都要有)每年能节省的汽油量不低于22.4万升,请问有哪几种购车方案?
(3)求(2)中最省钱的购买方案所需的购车款.