��Ŀ����
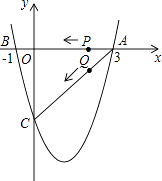
����Ŀ����ͼ����A��B������ֱ�Ϊ��0��8��������3��0������P�ӵ�A��������2��λ/����ٶ�������AO�����˶���ͬʱ��E�ӵ�B��������1��λ/����ٶ�������BO�����˶�����PEΪб�߹���Rt��PEC����ĸ����ʱ��˳����EC=2PC��������y=��2x2+bx+c�����㣨0��4��������1����2�������˶�ʱ��Ϊt�룮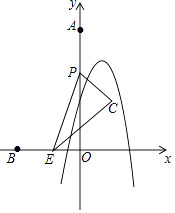
��1����������ߵı���ʽ��
��2����t=2ʱ�����C�����ꣻ
��3���ٵ�t��3ʱ�����C�����꣨�ú�t�Ĵ���ʽ��ʾ����
�����˶������У�����Cǡ�����ڸ��������ϣ���ֱ��д����������������t��ֵ��
���𰸡�
��1��
�⣺��������y=��2x2+bx+c�����㣨0��4��������1����2����
�� ![]()
�� ![]() ��
��
�������ߵĽ���ʽΪy=��2x2+4x+4��
��2��
�⣺��ͼ1�У�t=2ʱ��EO=1��OP=4����C��x��y������CH��x����H��PQ��HC��Q��

�ߡ�PCQ+��CPQ=90�㣬��ECH+��PCQ=90�㣬
���CPQ=��ECH���ߡ�Q=��CHE=90�㣬
���PCQ�ס�CEH��
�� ![]()
��EC=2PC��
�� ![]() =
= ![]() =
= ![]() ��
��
��x= ![]() ��y=
��y= ![]() ��
��
���C���꣨ ![]() ��
�� ![]() ��
��
��3��
�⣺����ͼ1�У���C��x��y������PO=8��2t��EH=3��t+x��CH=y��QC=8��2t��y��PQ=x��
�ߡ�PCQ�ס�CEH��
�� ![]()
��EC=2PC��
�� ![]() =
= ![]() =
= ![]() ��
��
��x= ![]() ��y=
��y= ![]() ��
��
���C���꣨ ![]() ��
�� ![]() ����
����
�ڵ�t��3ʱ�������C���������ϣ����� ![]() =��2��
=��2�� ![]() ��2+4
��2+4 ![]() +4��
+4��
���t=1��6����������
��t=1ʱ����C���������ϣ�
��3��t��4ʱ����ͼ���֪�������������ĵ�C���������ϣ�
��t��4ʱ����ͼ2�У���CH��x����H��PQ��HC��Q��

��C��x��y������PO=2t��8��EH=t��3��x��CH=��y��QC=2t��8+y��PQ=��x��
�ߡ�PCQ�ס�CEH��
�� ![]()
��EC=2PC��
�� ![]() =
= ![]() =
= ![]() ��
��
��x= ![]() ��y=
��y= ![]() ��
��
���C���꣨ ![]() ��
�� ![]() ����
����
�����C���������ϣ����� ![]() =��2��
=��2�� ![]() ��2+4
��2+4 ![]() +4��
+4��
���t=6��1����������
��t=6ʱ����C���������ϣ�
��������t=1��6sʱ����C ��������
����������1���ѣ�0��4��������1����2�����������߽���ʽy=��2x2+bx+c���з����鼴�ɽ�����⣮��2����ͼ1�У�t=2ʱ��EO=1��OP=4����C��x��y������CH��x����H��PQ��HC��Q���ɡ�PCQ�ס�CEH���� ![]() =
= ![]() =
= ![]() ���г������飬�ⷽ���鼴�ɽ�����⣮��3������ͼ1�У���C��x��y������PO=8��2t��EH=3��t+x��CH=y��QC=8��2t��y��PQ=x���ɡ�PCQ�ס�CEH����
���г������飬�ⷽ���鼴�ɽ�����⣮��3������ͼ1�У���C��x��y������PO=8��2t��EH=3��t+x��CH=y��QC=8��2t��y��PQ=x���ɡ�PCQ�ס�CEH���� ![]() =
= ![]() =
= ![]() ����EC=2PC���ɵ�
����EC=2PC���ɵ� ![]() =
= ![]() =
= ![]() ����t��ʾx��y���ɽ�����⣮�ڷ���������t��3ʱ���г����̼��ɽ�����⣮��3��t��4ʱ����Ȼ�����������ĵ�C���������ϣ���t��4ʱ����ͼ2�У���CH��x����H��PQ��HC��Q����C��x��y������PO=2t��8��EH=t��3��x��CH=��y��QC=2t��8+y��PQ=��x���ɡ�PCQ�ס�CEH���õ�
����t��ʾx��y���ɽ�����⣮�ڷ���������t��3ʱ���г����̼��ɽ�����⣮��3��t��4ʱ����Ȼ�����������ĵ�C���������ϣ���t��4ʱ����ͼ2�У���CH��x����H��PQ��HC��Q����C��x��y������PO=2t��8��EH=t��3��x��CH=��y��QC=2t��8+y��PQ=��x���ɡ�PCQ�ס�CEH���õ� ![]() =
= ![]() =
= ![]() ���ⷽ���鼴�ɵõ���C���꣬�����������ɽ�����⣮
���ⷽ���鼴�ɵõ���C���꣬�����������ɽ�����⣮

 �����������һ��һ��ϵ�д�
�����������һ��һ��ϵ�д�