题目内容
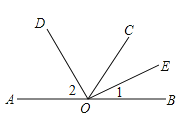
【题目】如图,O是直线AB上的一点,C是直线AB外的一点,OD是∠AOC的平分线,
OE是∠COB的平分线.
(1)已知∠1=23°,求∠2的度数;
(2)无论点C的位置如何改变,图中是否存在一个角,它的大小始终不变(∠AOB除外)?如果存在,求出这个角的度数;如果不存在,请说明理由.
【答案】(1)∠2=67°;(2)∠DOE的大小始终不变,等于90°;
【解析】
(1)由∠AOC与∠COB互补,且OD是∠AOC的平分线,OE是∠COB的平分线,利用角平分线定义及等式的性质求出∠2与∠1的度数之和,根据∠1的度数即可求出∠2的度数;
(2)∠DOE度数不变,度数为90度,理由为:根据∠AOC与∠COB互补,且OD是∠AOC的平分线,OE是∠COB的平分线,利用角平分线定义及等式的性质求出∠DOC与∠COE的度数之和为平角的一半,即可求出度数.
(1)∵OD是∠AOC的平分线,OE是∠COB的平分线,
∴∠2=∠DOC,∠1=∠COE,
∵∠AOC+∠COB=180°,
∴∠2+∠COD+∠1+∠COE=2(∠1+∠2)=180°,
∴∠1+∠2=90°,
∵∠1=23°,
∴∠2=67°;
(2)∠DOE度数不变,度数为90°,理由为:
∵OD是∠AOC的平分线,OE是∠COB的平分线,
∴∠2=∠DOC,∠1=∠COE,
∵∠AOC+∠COB=180°,
∴∠2+∠COD+∠1+∠COE=2(∠COD+∠COE)=180°,
∴∠COD+∠COE=90°,即∠DOE=90°.

练习册系列答案
相关题目