题目内容
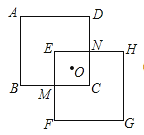
【题目】如图,在□ABCD中,∠ADC的平分线交AB于点E,∠ABC的平分线交CD于点F,求证:四边形EBFD是平行四边形.

【答案】见解析
【解析】试题分析:由在ABCD中,∠ABC的平分线交CD于点F,∠ADC的平分线交AB于点E,易证得∠ADE=∠CBF,从而得到△ADE≌△CBF,继而证得DF=EB,由DF∥BE,则可证得四边形EBFD是平行四边形.
试题解析:证明:∵四边形ABCD是平行四边形,∴AD=CB,∠A=∠C,∠ADC=∠ABC.
又∵∠ADE=![]() ∠ADC,∠CBF=
∠ADC,∠CBF=![]() ∠ABC,∴∠ADE=∠CBF,∴△ADE≌△CBF,∴AE=CF,∴AB﹣AE=CD﹣CF,即DF=EB.又∵DF∥EB,∴四边形EBFD是平行四边形.
∠ABC,∴∠ADE=∠CBF,∴△ADE≌△CBF,∴AE=CF,∴AB﹣AE=CD﹣CF,即DF=EB.又∵DF∥EB,∴四边形EBFD是平行四边形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目