题目内容
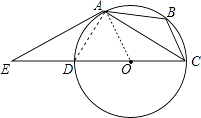
【题目】如图,⊙O是△ABC的外接圆,过点A作⊙O的切线与直径CD的延长线交于点E,已知AE=AC. 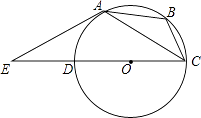
(1)求∠B的度数;
(2)若ED=1,求AE的长.
【答案】
(1)解:连接OA,
∵AE是⊙O的切线,
∴OA⊥AE,
∵AE=AC,OA=OC,
∴∠E=∠ACE=∠OAC,
∵∠BAC+∠E+∠ACE=180°,
∴90°+3∠E=180°,
∴∠E=∠ACE=∠OAC=30°,
∴∠AOC=90°+30°=120°,
∴ ![]() 的度数为120°,
的度数为120°, ![]() 的度数为240°,
的度数为240°,
∴∠B=120°
(2)解:∵在直角三角形OAE中,∠E=30°,
∴OE=2OA,
∵OA=OD,
∴OA=OD=OE=1,
∴OE=2,
∴AE= ![]() =
= ![]() .
.
【解析】(1)根据切线的性质得出OA⊥AE,然后根据等腰三角形的性质和三角形内角和定理得出∠E=∠ACE=∠OAC=30°,得出∠AOC=120°,从而求得 ![]() 的度数为120°,
的度数为120°, ![]() 的度数为240°,即可求得∠B=120°;(2)根据30°的直角三角形的性质得出OE=2OA=2OD,得出OD=ED=1,得出EO=2,根据勾股定理即可求得AE.
的度数为240°,即可求得∠B=120°;(2)根据30°的直角三角形的性质得出OE=2OA=2OD,得出OD=ED=1,得出EO=2,根据勾股定理即可求得AE.
【考点精析】本题主要考查了切线的性质定理的相关知识点,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.

练习册系列答案
相关题目