题目内容
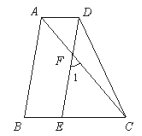
【题目】如图,AB∥DE,∠1=∠ACB,AC平分∠BAD,
(1)试说明: AD∥BC.
(2)若∠B=80°,求∠ADE的度数.
【答案】(1)证明见解析;(2)∠ADE=80°
【解析】
(1)根据平行线的性质与判定,两直线平行,即∠1=∠BAC,再利用角平分线的性质,得出∠1=∠DAC,进而得出∠DAC=∠ACB,即可得证;
(2)根据AB∥DE,AD∥BC,得出∠B=∠ADE,进而求出∠ADE的度数.
(1)证明:∵AB∥DE(已知),
∴∠1=∠BAC(两直线平行,同位角相等),
∵AC平分∠BAD(已知),
∴∠BAC=∠DAC,
∴∠1=∠DAC(等量代换),
∵∠1=∠ACB(已知),
∴∠DAC=∠ACB(等量代换),
∴AD∥BC(内错角相等,两直线平行).
(2)证明:∵AB∥DE,AD∥BC,
∴∠B=∠DEC,∠DEC=∠ADE,
∴∠B=∠ADE,
∵∠B=80°,
∴∠ADE=80°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目