题目内容
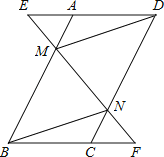
【题目】已知，如图，在ABCD中，延长DA到点E，延长BC到点F，使得AE=CF，连接EF，分别交AB，CD于点M，N，连接DM，BN．
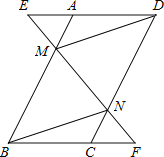
（1）求证：△AEM≌△CFN；
（2）求证：四边形BMDN是平行四边形．
【答案】见解析
【解析】
试题分析：（1）先根据平行四边形的性质可得出AD∥BC，∠DAB=∠BCD，再根据平行线的性质及补角的性质得出∠E=∠F，∠EAM=∠FCN，从而利用ASA可作出证明；
（2）根据平行四边形的性质及（1）的结论可得BM
DN，则由有一组对边平行且相等的四边形是平行四边形即可证明．
证明：（1）四边形ABCD是平行四边形，
∴∠DAB=∠BCD，
∴∠EAM=∠FCN，
又∵AD∥BC，
∴∠E=∠F．
∵在△AEM与△CFN中，
，
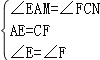∴△AEM≌△CFN（ASA）；
（2）∵四边形ABCD是平行四边形，
∴ABCD，
又由（1）得AM=CN，
∴BMDN，
∴四边形BMDN是平行四边形．
练习册系列答案
相关题目
【题目】某商店需要购进A．B两种商品共160件，其进价和售价如表：
A | B | |
进价（元/件） | 15 | 35 |
售价（元/件） | 20 | 45 |
（1）当A．B两种商品分别购进多少件时，商店计划售完这批商品后能获利1100元；
（2）若商店计划购进A种商品不少于66件，且销售完这批商品后获利多于1260元，请你帮该商店老板预算有几种购货方案？获利最大是多少元？
