题目内容
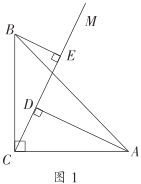
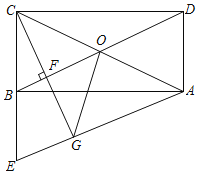
【题目】如图,在矩形ABCD中,AC、BD相交于点O,过点A作BD的平行线AE交CB的延长线于点E.
(1)求证:BE=BC;
(2)过点C作CF⊥BD于点F,并延长CF交AE于点G,连接OG.若BF=3,CF=6,求四边形BOGE的周长.
【答案】(1)详见解析;(2)3![]() +21.
+21.
【解析】
(1)利用平行线等分线段定理证明即可.
(2)根据勾股定理得BC=![]() ,易证△CBF∽△DBC,得BD=15,根据矩形的性质和直角三角形的性质得OG=
,易证△CBF∽△DBC,得BD=15,根据矩形的性质和直角三角形的性质得OG=![]() ,利用平行线等分线段定理得BE=3
,利用平行线等分线段定理得BE=3![]() ,由中位线的性质得EG=6,进而即可求解.
,由中位线的性质得EG=6,进而即可求解.
(1)∵四边形ABCD是矩形,
∴OC=OA,
∵OB∥AE,
∴BC=BE;
(2)∵CF⊥BD,
∴∠CFB=90°,
在Rt△BCF中,BC=![]() ,
,
∵四边形ABCD是矩形,
∴∠BCD=90°=∠BFC,AC=BD,
∵∠CBF=∠DBC,
∴△CBF∽△DBC,
∴![]() ,
,
∴BD=![]() =15,OB=OD=
=15,OB=OD=![]() ,
,
∴AC=BD=15,
∵CF⊥BD,BD∥AE,
∴CG⊥AE,
∴∠AGC=90°,
∵OC=OA,
∴OG=![]() AC=
AC=![]() ,
,
∵OC=OA,OF∥AG,
∴CF=FG,
∴BC=BE=3![]() ,
,
∴EG=2BF=6,
∴四边形BOGE的周长=3![]() +6+
+6+![]() +
+![]() =3
=3![]() +21.
+21.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目