��Ŀ����
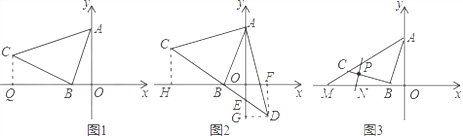
����Ŀ����ͼ1����ֱ֪��y=2x+2��y�ᡢx��ֱ���A��B���㣬��BΪֱ�Ƕ����ڵڶ�����������Rt��ABC ��
��1�����C�����꣬�����ֱ��AC�Ĺ�ϵʽ��
��2����ͼ2��ֱ��CB��y����E����ֱ��CB��ȡһ��D������AD����AD=AC����֤��BE=DE��
��3����ͼ3���ڣ�1���������£�ֱ��AC��x����M��P��![]() ��k�����߶�BC��һ�㣬���߶�BM���Ƿ����һ��N��ʹ��BPN�����������BCM�����
��k�����߶�BC��һ�㣬���߶�BM���Ƿ����һ��N��ʹ��BPN�����������BCM�����![]() �������ڣ��������N�����ꣻ�������ڣ���˵�����ɣ�
�������ڣ��������N�����ꣻ�������ڣ���˵�����ɣ�


���𰸡���1��C����3��1����ֱ��AC��y=![]() x+2����2��֤������������3��N����
x+2����2��֤������������3��N����![]() ��0����
��0����
�������������������1����CQ��x�ᣬ����ΪQ����������֤����ABO�ա�BCQ���Ӷ����CQ=OB=1���ɵ�C����3��1�����ô���ϵ��������ֱ��AC�Ľ���ʽy=![]() x+2����2����CH��x����H��DF��x����F��DG��y����G��֤����BCH�ա�BDF����BOE�ա�DGE���ɵ�BE=DE����3�������ֱ��BC�Ľ���ʽ���Ӷ�ȷ����P�����꣬������ڵ�Nʹֱ��PNƽ����BCM�������Ȼ������BN�ij����Ƚ�BM,BN�Ĵ�С���жϵ�N�Ƿ����߶�BM�ϼ��ɣ�
x+2����2����CH��x����H��DF��x����F��DG��y����G��֤����BCH�ա�BDF����BOE�ա�DGE���ɵ�BE=DE����3�������ֱ��BC�Ľ���ʽ���Ӷ�ȷ����P�����꣬������ڵ�Nʹֱ��PNƽ����BCM�������Ȼ������BN�ij����Ƚ�BM,BN�Ĵ�С���жϵ�N�Ƿ����߶�BM�ϼ��ɣ�
����������⣺��1����ͼ1����CQ��x�ᣬ����ΪQ��
���OBA+��OAB=90������OBA+��QBC=90����
���OAB=��QBC��
����AB=BC����AOB=��Q=90����
���ABO�ա�BCQ��
��BQ=AO=2��OQ=BQ+BO=3��CQ=OB=1��
��C����3��1����
��A��0��2����C����3��1��
��֪��ֱ��AC��y=![]() x+2��
x+2��
��2����ͼ2����CH��x����H��DF��x����F��DG��y����G��
��AC=AD��AB��CB��
��BC=BD��
���BCH�ա�BDF��
��BF=BH=2��
��OF=OB=1��
��DG=OB��
���BOE�ա�DGE��
��BE=DE��
��3����ͼ3��ֱ��BC��y=��![]() x��
x��![]() ��P��
��P��![]() ��k�����߶�BC��һ�㣬
��k�����߶�BC��һ�㣬
��P����![]() ��
��![]() ������y=
������y=![]() x+2֪M����6��0����
x+2֪M����6��0����
��BM=5����S��BCM=![]() ��
��
������ڵ�Nʹֱ��PNƽ����BCM�������
��![]() BN��
BN��![]() =
=![]() ��
��![]() ��
��
��BN=![]() ��ON=
��ON=![]() ��
��
��BN��BM��
����N���߶�BM�ϣ�
��N����![]() ��0����
��0����

 ������ϵ�д�
������ϵ�д�