题目内容
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于60元,经市场调查,每天的销售量y(单位:千克)与每千克售价x(单位:元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 45 | 50 | 60 |
销售量y(千克) | 110 | 100 | 80 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为w(单位:元),则当每千克售价x定为多少元时,超市每天能获得的利润最大?最大利润是多少元?
【答案】(1)y=﹣2x+200 (40≤x≤60);(2)售价为60元时获得最大利润,最大利润是1600元.
【解析】
(1)待定系数法求解可得;
(2)根据“总利润=每千克利润×销售量”可得函数解析式,将其配方成顶点式即可得最值情况.
解:(1)设y=kx+b,
将(50,100)、(60,80)代入,得:![]() ,
,
解得:![]() ,
,
∴y=﹣2x+200 (40≤x≤60);
(2)w=(x﹣40)(﹣2x+200)
=﹣2x2+280x﹣8000
=﹣2(x﹣70)2+1800,
∵40≤x≤60,
∴当x=60时,w取得最大值为1600,
答:w与x之间的函数表达式为W=﹣2x2+280x﹣8000,售价为60元时获得最大利润,最大利润是1600元.

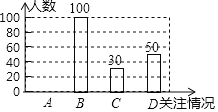
【题目】2019年2月18日,“时代楷模”、伏牛山里的好教师﹣﹣张玉滚当选“感动中国”2018年度人物,在中原大地引起强烈反响.为了解学生对张玉滚事迹的知晓情况,某数学课外兴趣小组在本校学生中开展了专题调查活动,随机抽取了部分学生进行问卷调查,根据学生的答题情况,将结果分为A,B,C,D四类,将调查的数据整理后绘制成如下统计表及条形统计图(均不完整):
关注情况 | 频数 | 频率 |
A.非常了解 | m | 0.1 |
B.比较了解 | 100 | 0.5 |
C.基本了解 | 30 | n |
D.不太了解 | 50 | 0.25 |
根据以上信息解答下列问题:
(1)在这次抽样调查中,一共抽查了 名学生;
(2)统计表中,m= ,n= ;
(3)请把条形统计图补充完整;
(4)该校共有学生1500名,请你估算该校学生中对张玉滚事迹“非常了解“和“比较了解”的学生共有多少名.