题目内容
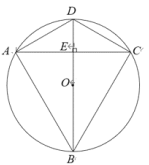
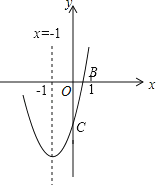
【题目】已知抛物线![]() 经过点
经过点![]() 和
和 ![]() ,与
,与![]() 轴交于另一点
轴交于另一点![]() ,顶点为
,顶点为![]() .
.
(1)求抛物线的解析式,并写出![]() 点的坐标;
点的坐标;
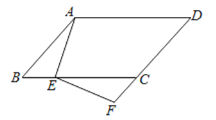
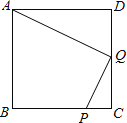
(2)如图,点![]() 分别在线段
分别在线段![]() 上(
上(![]() 点不与
点不与![]() 重合),且
重合),且![]() ,则
,则![]() 能否为等腰三角形?若能,求出
能否为等腰三角形?若能,求出![]() 的长;若不能,请说明理由;
的长;若不能,请说明理由;
(3)若点![]() 在抛物线上,且
在抛物线上,且![]() ,试确定满足条件的点
,试确定满足条件的点![]() 的个数.
的个数.

【答案】(1)![]() ;(2)可能,
;(2)可能,![]() 的长为
的长为![]() 或
或![]() ;(3)当
;(3)当![]() 时,满足条件的点
时,满足条件的点![]() 的个数有
的个数有![]() 个,当
个,当![]() 时,满足条件的点
时,满足条件的点![]() 的个数有
的个数有![]() 个,当
个,当![]() 时,满足条件的点
时,满足条件的点![]() 的个数有
的个数有![]() 个(此时点
个(此时点![]() 在
在![]() 的左侧).
的左侧).
【解析】
(1)利用待定系数法,转化为解方程组即可解决问题.
(2)可能分三种情形①当![]() 时,②当
时,②当![]() 时,③当
时,③当![]() 时,分别求解即可.
时,分别求解即可.
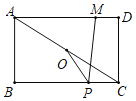
(3)如图2中,连接![]() ,当点
,当点![]() 在线段
在线段![]() 的右侧时,作
的右侧时,作![]() 于
于![]() ,连接
,连接![]() .设
.设![]() ,构建二次函数求出
,构建二次函数求出![]() 的面积的最大值,再根据对称性即可解决问题.
的面积的最大值,再根据对称性即可解决问题.
(1)由题意: 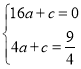
解得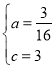
![]() 抛物线的解析式为
抛物线的解析式为![]() ,
,
![]() 顶点
顶点![]() 坐标
坐标![]() .
.
(2)可能.如图1,
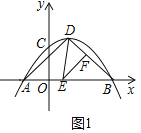
![]()
![]()
①当![]() 时,
时,![]()
![]() ,此时
,此时![]() 与
与![]() 重合,与条件矛盾,不成立.
重合,与条件矛盾,不成立.
②当![]() 时,
时,
又![]() ,
,
![]() ,
,
![]()
③当![]() 时,
时,![]()
![]()
![]()
![]() ,
,
![]()
![]() ,
,
![]()
答:当![]() 的长为
的长为![]() 或
或![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.
(3)如图2中,连接![]() ,当点
,当点![]() 在线段
在线段![]() 的右侧时,作
的右侧时,作![]() 于
于![]() ,连接
,连接![]() .设
.设![]()
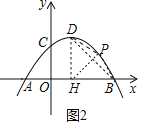
则![]()
![]()
![]()
![]()
![]()
![]() 时,
时,![]() 的面积的最大值为
的面积的最大值为![]() ,
,
![]()
![]() 当点
当点![]() 在
在![]() 的右侧时,
的右侧时,![]() 的最大值
的最大值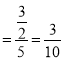 ,
,
观察图象可知:当![]() 时,满足条件的点
时,满足条件的点![]() 的个数有
的个数有![]() 个,
个,
当![]() 时,满足条件的点
时,满足条件的点![]() 的个数有
的个数有![]() 个,
个,
当![]() 时,满足条件的点
时,满足条件的点![]() 的个数有
的个数有![]() 个(此时点
个(此时点![]() 在
在![]() 的左侧).
的左侧).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目