Question

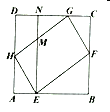
【题目】如图，四边形中，平分.

（1）求证：；

（2）求证：点是的中点；

（3）若，求的长.

Answer 1

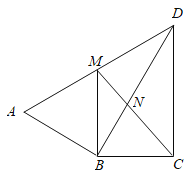
【答案】（1）见解析；（2）见解析；（3）

【解析】

（1）通过证明△ABD∽△BCD，可得，可得结论；

（2）通过和相似得出∠MBD=∠MDB，在利用同角的余角相等得出∠A=∠ABM，由等腰三角形的性质可得结论；

（3）由平行线的性质可证∠MBD=∠BDC，即可证AM=MD=MB=4，由BD2=ADCD和勾股定理可求MC的长，通过证明△MNB∽△CND，可得.

解：（1）证明：∵DB平分∠ADC，
∴∠ADB=∠CDB，且∠ABD=∠BCD=90°，
∴△ABD∽△BCD，

∴，

∴BD2=ADCD

（2）证明：∵，

∴∠MBD=∠BDC，∠MBC=90°，

∵∠MDB=∠CDB，

∴∠MBD=∠MDB，

∴MB=MD，

∵∠MBD+∠ABM=90°，

∴∠ABM=∠CBD，

∵∠CBD=∠A，

∴∠A=∠ABM，

∴MA=MB，

∴MA=MD，

即M为AD中点；

（3）∵BM∥CD
∴∠MBD=∠BDC
∴∠ADB=∠MBD，且∠ABD=90°
∴BM=MD，∠MAB=∠MBA
∴BM=MD=AM=4
∵BD2=ADCD，且CD=6，AD=8，
∴BD2=48，
∴BC2=BD2-CD2=12
∴MC2=MB2+BC2=28
∴MC=，

∵BM∥CD
∴△MNB∽△CND

∴，且MC=，

∴.