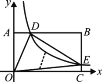
��Ŀ����
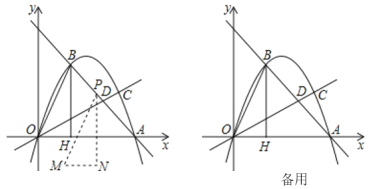
����Ŀ����ͼ��ֱ��y����x+m��������y��ax2+bx��������A��6��0������B����B��BH��ֱx����H��OA��3OH��ֱ��OC��������AB�ν��ڵ�C��
��1���������ߵĽ���ʽ��
��2������C����������![]() ʱ����ֱ��OC��ֱ��AB�Ľ���D�����ꣻ
ʱ����ֱ��OC��ֱ��AB�Ľ���D�����ꣻ
��3���ڣ�2���������½���OBH��BA����ƽ�Ƶ���MPN������Pʼ�����߶�AB�ϣ�����MPN����OAC����������������ֵ��
���𰸡���1��y��-![]() x2+3x����2��(4��2)����3��
x2+3x����2��(4��2)����3��![]()
��������
��1�������ֱ��AB�Ľ���ʽ�������B���꣬�ٽ�A��B���������y��ax2+bx���ɣ�
��2�����ֱ��AC�Ľ���ʽ��������ֱ��OC��ֱ��AB�Ľ���ʽ���ɣ�
��3����PM��OC��PA�ֱ���G��H��PN��OC��OA�ֱ���K��F���ֱ����ֱ��OB��PM��OC�Ľ���ʽ���ٷֱ��ú�a�Ĵ���ʽ��ʾ��H��G��E��F�����꣬����������ۣ��������MPN���OAC����������������ֵ��
�⣺��1����ֱ��y����x+m��A��6��0����
�ੁ6+m��0��
��m��6��
��yAB����x+6��
��OA��3OH��
��OH��2��
��yAB����x+6�У���x��2ʱ��y��4��
��B��2��4����
��A��6��0����B��2��4������y��ax2+bx��
�ã�![]() ��
��
��ã�a����![]() ��b��3��
��b��3��
�������ߵĽ���ʽΪy��-![]() x2+3x��
x2+3x��
��2����ֱ��OC��������AB�ν��ڵ�C���ҵ�C����������![]() ��
��
��![]() ����
����![]() x2+3x��
x2+3x��
��ã�x1��1����ȥ����x2��5��
��C��5��![]() ����
����
��yOC��kx��
��C��5��![]() �����룬
�����룬
�ã�k��![]() ��
��
��yOC��![]() x��
x��
����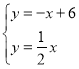 ��
��
��ã�x��4��y��2��
���D��������4��2����
��3����ֱ��OB�Ľ���ʽΪyOB��mx����P����Ϊ��a����a+6����
����B��2��4�����룬
�ã�m��2��
��yOB��2x��
��ƽ��֪��PM��OB��
����ֱ��PM�Ľ���ʽΪyPM��2x+n��
��P��a����a+6�����룬
���a+6��2a+n��
��n��6��3a��
��yPM��2x+6��3a��
��PM��OC��PA�ֱ���G��H��PN��OC��OA�ֱ���K��F��
����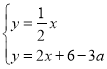 ��
��
��ã�x��2a��4��y��a��2��
��G��2a��4��a��2����yG��a��2��
��yPM��2x+6��3a��
��y��0ʱ��x��![]() ��
��
��E��![]() ��0����OE��
��0����OE��![]() ��
��
�ߵ�P�ĺ�����Ϊa��
��K��a��![]() a����F��a��0����
a����F��a��0����
��OF��a��KF��![]() a��
a��
���MPN���OAC�����������ΪS��
�ٵ�0��a��4ʱ��
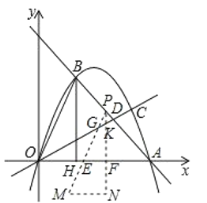
S��S��OFK��S��OEG��
��![]() ��a��
��a��![]() a��
a��![]() ��
��![]() ����a��2����
����a��2����
����![]() a2+3a��3
a2+3a��3
����![]() ��a��3��2+
��a��3��2+![]() ��
��
�ߩ�![]() ��0�����ݶ��κ�����ͼ�����ʿ�֪��
��0�����ݶ��κ�����ͼ�����ʿ�֪��
�൱a��3ʱS�����ֵ![]() ��
��
�ڵ�4��a��6ʱ��
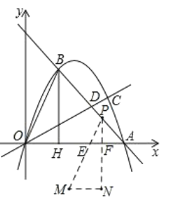
S��S��PEF
��![]() EFPF
EFPF
��![]() ��a��
��a��![]() a+3������a+6��
a+3������a+6��
��![]()
��![]() ��
��
��![]() �����ݶ��κ�����ͼ������֪����a��4ʱ��S�����ֵ1��
�����ݶ��κ�����ͼ������֪����a��4ʱ��S�����ֵ1��
��![]()
���MPN���OAC����������������ֵΪ![]() ��
��

 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д� �����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
�����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д� �����ҵ�����������ѧ���ӳ�����ϵ�д�
�����ҵ�����������ѧ���ӳ�����ϵ�д�