题目内容
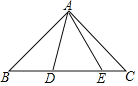
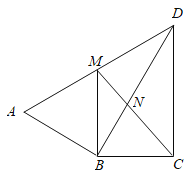
【题目】如图,平行四边形![]() 的四个顶点分别在正方形
的四个顶点分别在正方形![]() 的四条边上.
的四条边上.![]() ,分别交
,分别交![]() ,
,![]() ,
,![]() 于点
于点![]() ,
,![]() ,
,![]() ,且
,且![]() .要求得平行四边形
.要求得平行四边形![]() 的面积,只需知道一条线段的长度.这条线段可以是( )
的面积,只需知道一条线段的长度.这条线段可以是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
根据图形证明△AOE≌△COG,作KM⊥AD,证明四边形DKMN为正方形,再证明Rt△AEH≌Rt△CGF,Rt△DHG≌Rt△BFE,设正方形![]() 边长为a,CG=MN=x,根据正方形的性质列出平行四边形
边长为a,CG=MN=x,根据正方形的性质列出平行四边形![]() 的面积的代数式,再化简整理,即可判断.
的面积的代数式,再化简整理,即可判断.
连接AC,EG,交于O点,
∵四边形![]() 是平行四边形,四边形
是平行四边形,四边形![]() 是正方形,
是正方形,
∴GO=EO,AO=CO,
又∠AOE=∠COG
∴△AOE≌△COG,
∴GC=AE,
∵NE∥AD,
∴四边形AEND为矩形,
∴AE=DN,
∴DN=GC=MN
作KM⊥AD,
∴四边形DKMN为正方形,
在Rt△AEH和Rt△CGF中,
![]()
∴Rt△AEH≌Rt△CGF,
∴AH=CF,
∵AD-AH=BC-CF
∴DH=BF,
同理Rt△DHG≌Rt△BFE,
设CG=MN=x,
设正方形![]() 边长为a
边长为a
则S△HDG=![]() DH×x+
DH×x+![]() DG×x=S△FBE
DG×x=S△FBE
S△HAE=![]() AH×x =S△GCF
AH×x =S△GCF
S平行四边形EFGH=a2-2S△HDG-2S△HAE= a2-(DH+DG+AH)×x,
∵DG=a-x
∴S平行四边形EFGH= a2-(a+a-x)×x= a2-2ax+x2= (a-x)2
故只需要知道a-x就可以求出面积
BE=a-x,故选C.

练习册系列答案
相关题目
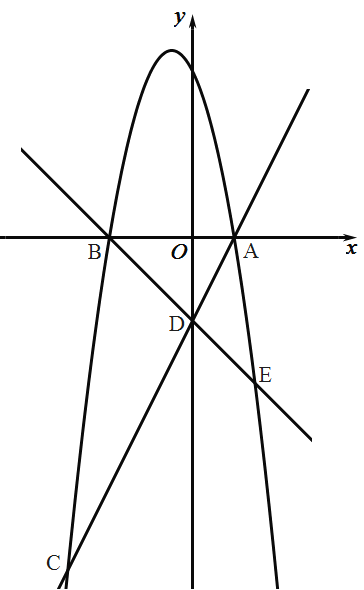
【题目】二次函数![]() (
(![]() ,
,![]() ,
,![]() 为常数,且
为常数,且![]() )中的
)中的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
以下结论:
①二次函数![]() 有最小值为
有最小值为![]() ;
;
②当![]() 时,
时,![]() 随
随![]() 的增大而增大;
的增大而增大;
③二次函数![]() 的图象与
的图象与![]() 轴只有一个交点;
轴只有一个交点;
④当![]() 时,
时,![]() .
.
其中正确的结论有( )个
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()