题目内容
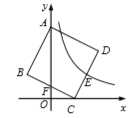
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() 且与反比例函数
且与反比例函数![]() 在第一象限的图象交于点
在第一象限的图象交于点![]() 轴于点
轴于点![]() .
.
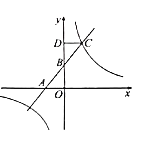
![]() 根据函数图象,直接写出当反比例函数
根据函数图象,直接写出当反比例函数![]() 的函数值
的函数值![]() 时,自变量
时,自变量![]() 的取值范围;
的取值范围;
![]() 动点
动点![]() 在
在![]() 轴上,
轴上,![]() 轴交反比例函数
轴交反比例函数![]() 的图象于点
的图象于点![]() .若
.若![]() .求点
.求点![]() 的坐标.
的坐标.
【答案】![]()
![]() 或
或![]() .
.![]()
![]() 或
或![]() .
.
【解析】
(1)根据函数图象即可得出答案
(2)由已知条件得出点C的坐标为(2,5),再利用B,C的坐标求出直线AC的解析式,可求出A的坐标为(-2,0),由已知条件得出三角形POQ的面积为5,则三角形PAC的面积为10,再利用三角形面积公式可求出PA的值,进而确定P点的坐标.
解: ![]() 由已知图象得出,
由已知图象得出,
当![]() 时,y<0,
时,y<0,
当x=2时,y=5,∴![]() 时,
时,![]()
所以,x的取值范围为:![]() 或
或![]() .
.
![]()
![]() 轴于点
轴于点![]() .
.![]() 点的横坐标为
点的横坐标为![]() .
.
把![]() 代入反比例函数
代入反比例函数![]() ,得
,得![]() .
.
设直线![]() 的解析式为
的解析式为![]() ,
,
把![]() 代入
代入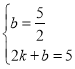 ,得
,得![]()
![]() 直线
直线![]() 的解析式为
的解析式为![]()
令![]() ,解得
,解得![]() .
.
![]()
![]() 轴,点
轴,点![]() 在反比例函数
在反比例函数![]() 的图象上
的图象上
![]()
![]()
![]()
则![]() ,
,
![]()
![]() 或
或![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】二次函数![]() (
(![]() ,
,![]() ,
,![]() 为常数,且
为常数,且![]() )中的
)中的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
以下结论:
①二次函数![]() 有最小值为
有最小值为![]() ;
;
②当![]() 时,
时,![]() 随
随![]() 的增大而增大;
的增大而增大;
③二次函数![]() 的图象与
的图象与![]() 轴只有一个交点;
轴只有一个交点;
④当![]() 时,
时,![]() .
.
其中正确的结论有( )个
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()