题目内容
【题目】在正方形ABCD中,P是BC上一点,且BP=3PC,Q是CD的中点.
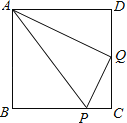
(1)求证:△ADQ∽△QCP;
(2)若PQ=3,求AP的长.
【答案】(1)见解析;(2)3![]()
【解析】
(1)在所要求证的两个三角形中,已知的等量条件为:∠D=∠C=90°,若证明两三角形相似,可证两个三角形的对应直角边成比例;
(2)证明AQ=2PQ,AQ⊥PQ即可解决问题.
(1)证明:∵四边形ABCD是正方形,
∴AD=CD,∠C=∠D=90°;
又∵Q是CD中点,
∴CQ=DQ=![]() AD;
AD;
∵BP=3PC,
∴CP=![]() AD,
AD,
∴![]() =
=![]() =
=![]() ,
,
又∵∠C=∠D=90°,
∴△ADQ∽△QCP;
(2)由(1)知,△ADQ∽△QCP,![]() =
=![]() =
=![]() ,
,
∴AQ=2PQ,
∵PQ=3,
∴AQ=6,
∵△ADQ∽△QCP,
∴∠AQD=∠QPC,∠DAQ=∠PQC,
∴∠PQC+∠DQA=DAQ+AQD=90°,
∴AQ⊥QP,
∴∠AQP=90°,
∴PA=![]() =3
=3![]() .
.


练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目