题目内容
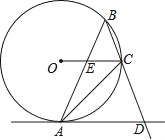
【题目】如图⊙O是△ABC的外接圆,∠ABC=45°,延长BC于D,连接AD,使得AD∥OC,AB交OC于E.
(1)求证:AD与⊙O相切;
(2)若AE=2![]() ,CE=2.求⊙O的半径和AB的长度.
,CE=2.求⊙O的半径和AB的长度.
【答案】(1)见解析;(2)AB=![]() .
.
【解析】
(1)连接OA,要证明切线,只需证明OA⊥AD,根据AD∥OC,只需得到OA⊥OC,根据圆周角定理即可证明;
(2)设⊙O的半径为R,则OA=R,OE=R-2,AE=2![]() ,在Rt△OAE中根据勾股定理可计算出R=4;作OH⊥AB于H,根据垂径定理得AH=BH,再利用面积法计算出OH=
,在Rt△OAE中根据勾股定理可计算出R=4;作OH⊥AB于H,根据垂径定理得AH=BH,再利用面积法计算出OH=![]() ,然后根据勾股定理计算出AH=
,然后根据勾股定理计算出AH=![]() ,再利用垂径定理得出AB=2AH═
,再利用垂径定理得出AB=2AH═![]() .
.
(1)连接OA,
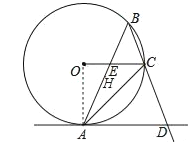
∵∠ABC=45°,
∴∠AOC=2∠ABC=90°,
∴OA⊥OC;
又∵AD∥OC,
∴OA⊥AD,
∴AD是⊙O的切线.
(2)设⊙O的半径为R,则OA=R,OE=R﹣2,AE=2![]() ,
,
在Rt△OAE中,∵AO2+OE2=AE2,
∴R2+(R﹣2)2=(2![]() )2,解得R=4,
)2,解得R=4,
作OH⊥AB于H,如图,
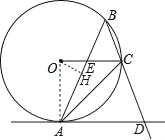
OE=OC﹣CE=4﹣2=2,
则AH=BH,
∵![]() OHAE=
OHAE=![]() OEOA,
OEOA,
∴OH=![]() =
=![]() =
=![]() ,
,
在Rt△AOH中,AH=![]() =
=![]() ,
,
∵OH⊥AB,
∴AB=2AH=![]() .
.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
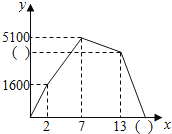
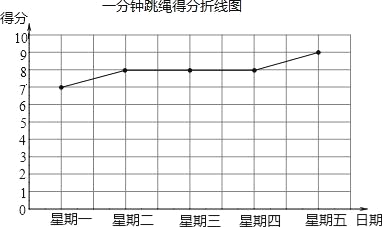
【题目】我市2013年体育中考考试方案公布后,同学们将根据自己平的运动成绩确定自己的报考项目,下面是小亮同学近期在两个项目中连续五次测试的(得分情况得分统计表得分折线图)
立定跳远测试日期 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
得分 | 7 | 10 | 8 | 9 | 6 |
(1)请根据图表信息,分别计算小亮这两个项目测试成绩的平均数和方差;
(2)根据以上信息,你认为在立定跳远和一分钟跳绳这两个项目中,小亮应选择哪个项目作为体育考试的报考项目?并简述理由.