题目内容

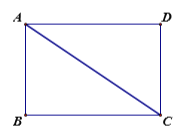
【题目】已知，如图：一张矩形纸片，，，为边上一动点，将矩形沿折叠，要使点落在上，则折痕的长度是________；若点落在上，则折痕与的位置关系是__________.若翻折后点的对应点是点，连接，则在点运动的过程中，的最小值是______.

【答案】 垂直 4

【解析】

由折叠的性质和矩形的性质得出四边形是正方形，然后利用勾股定理即可求BE的长度；由折叠的性质即可得出若点落在上，则折痕与的位置关系；分析得出

当在BD上时，的长度最小，然后利用即可求解．

如图，

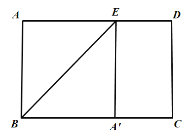
由折叠的性质可知， ，

∵四边形ABCD是矩形，

∴ ，

∴四边形是正方形，

，

；

若点落在上，根据折叠的性质可知，BE垂直平分，所以折痕与的位置关系是垂直；

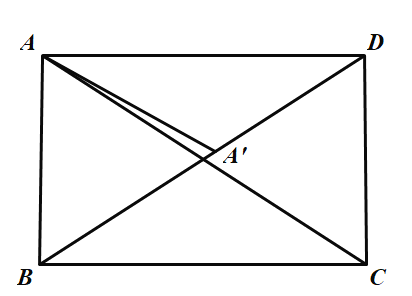
如图，当在BD上时，的长度最小，

，

．

，

，

∴的最小值是4．

故答案为：，垂直，4．

练习册系列答案
相关题目

【题目】如图，已知△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC的中点，两边PE、PF分别交AB、AC于点E、F，给出以下五个结论：①AE=CF；②∠APE=∠CPF；③△EPF是等腰直角三角形；④EF=AP；⑤．当∠EPF在△ABC内绕顶点P旋转时（点E不与点A、B重合），上述结论中始终正确的序号有 ．

【题目】如图，AB是半圆O的直径，E是弧BC的中点，OE交弦BC于点D，点F为OE的延长线上一点且OC2=OD·OF.

（1）求证：CF为⊙O的切线.

（2）已知DE=2， .

①求⊙O的半径；②求sin∠BAD的值

【题目】如图1，在矩形中，，，点从点出发，沿路线运动，到点停止；点从点出发，沿A运动，到点停止，若点、点同时出发，点的速度为每秒，点的速度为每秒，秒时点、点同时改变速度，点的速度变为每秒，点的速度变为每秒，如图2是点出发秒后的面积与的函数关系图象，图3是点出发秒后的面积与的函数关系图象，根据图象：

（1）点经过______秒运动到点，此时的面积为______；点经过______秒运动到点；

（2）______秒，______，______；

（3）设点离开点的路程为，点到点还需要走的路程为，请分别写出改变速度后、与出发后的运动时间（秒）的函数关系式；

（4）直接写出与相遇时的值．

【题目】已知关于x的一元二次方程x2+（2k+3）x+k2＝0有两个不相等的实数根x1，x2．若＝﹣1，则k的值为_____．

【题目】有大小两种货车，3辆大货车与2辆小货车一次可以运货21吨，2辆大货车与4辆小货车一次可以运货22吨．

（1）每辆大货车和每辆小货车一次各可以运货多少吨？

（2）现有这两种货车共10辆，要求一次运货不低于35吨，则其中大货车至少多少辆？（用不等式解答）

（3）日前有23吨货物需要运输，欲租用这两种货车运送，要求全部货物一次运完且每辆车必须装满．已知每辆大货车一次运货租金为300元，每辆小货车一次运货租金为200元，请列出所有的运输方案井求出最少租金．

【题目】如图，已知等腰，，平分，为上一动点，作平行，交于F，在上取一点，使得，连接.

（1）根据题意补全图形；

（2）求证四边形是平行四边形；

（3）若，写出一个的度数，使得四边形是菱形.

【题目】解方程：

（1）（用配方法）；

（2） ；

（3）；

（4）(500－20x)（10+x）=6000．

【题目】如图，方格纸中的每个小方格都是边长为1个单位的正方形．Rt△ABC的顶点均在格点上，建立平面直角坐标系后，点A的坐标为（﹣4，1），点B的坐标为（﹣1，1）．

（1）先将Rt△ABC向右平移5个单位，再向下平移1个单位后得到Rt△A1B1C1．试在图中画出图形Rt△A1B1C1，并写出A1的坐标；

（2）将Rt△A1B1C1绕点A1顺时针旋转90°后得到Rt△A2B2C2，试在图中画出图形Rt△A2B2C2．并计算Rt△A1B1C1在上述旋转过程中C1所经过的路程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网