题目内容
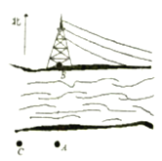
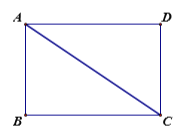
【题目】如图1,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从
从![]() 点出发,沿
点出发,沿![]() 路线运动,到
路线运动,到![]() 点停止;点
点停止;点![]() 从
从![]() 点出发,沿
点出发,沿![]() A运动,到
A运动,到![]() 点停止,若点
点停止,若点![]() 、点
、点![]() 同时出发,点
同时出发,点![]() 的速度为每秒
的速度为每秒![]() ,点
,点![]() 的速度为每秒
的速度为每秒![]() ,
,![]() 秒时点
秒时点![]() 、点
、点![]() 同时改变速度,点
同时改变速度,点![]() 的速度变为每秒
的速度变为每秒![]() ,点
,点![]() 的速度变为每秒
的速度变为每秒![]() ,如图2是点
,如图2是点![]() 出发
出发![]() 秒后
秒后![]() 的面积
的面积![]() 与
与![]() 的函数关系图象,图3是点
的函数关系图象,图3是点![]() 出发
出发![]() 秒后
秒后![]() 的面积
的面积![]() 与
与![]() 的函数关系图象,根据图象:
的函数关系图象,根据图象:
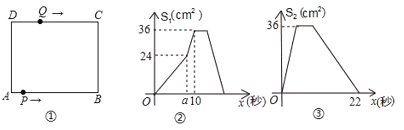
(1)点![]() 经过______秒运动到
经过______秒运动到![]() 点,此时
点,此时![]() 的面积为______;点
的面积为______;点![]() 经过______秒运动到
经过______秒运动到![]() 点;
点;
(2)![]() ______秒,
______秒,![]() ______
______![]() ,
,![]() ______
______![]() ;
;
(3)设点![]() 离开点
离开点![]() 的路程为
的路程为![]() ,点
,点![]() 到点
到点![]() 还需要走的路程为
还需要走的路程为![]() ,请分别写出改变速度后
,请分别写出改变速度后![]() 、
、![]() 与出发后的运动时间
与出发后的运动时间![]() (秒)的函数关系式;
(秒)的函数关系式;
(4)直接写出![]() 与
与![]() 相遇时
相遇时![]() 的值.
的值.
【答案】(1)10;36;6;(2)8;2;1;(3)y1=2x-8(x>8);y2==22-x(x>8);(4)10
【解析】
(1)先求得点P到达B点时△APD的面积,然后结合图2中的图像分析求得时间,然后求出点Q到达点C时△AQD的面积,然后结合Q的运动速度分析求得时间;
(2)根据题意和S△APD求出a,b,c的值;
(3)首先求出y1,y2关于x的等量关系;
(4)根据题意可得y1=y2求出x的值;
解:(1)由题意可知![]() ,
,![]() ,点
,点![]() 的速度为每秒
的速度为每秒![]() ,点
,点![]() 的速度为每秒
的速度为每秒![]() ,
,
∴在矩形ABCD中,AD=BC=6
∴点![]() 运动到
运动到![]() 点时,
点时,![]()
∴由图2可知,当![]() 时,x=10,即点P运动到点B需要10秒
时,x=10,即点P运动到点B需要10秒
又由图2可知,当![]() 时,
时,![]()
∴此时AP=8,即8秒时P,Q同时改变速度
同理,当点Q运动到点C时,![]()
∴点Q到达点C的时间为![]()
故答案为:10;36;6;
(2)观察图象得,S△APQ=![]() PAAD=
PAAD=![]() ×(1×a)×6=24,
×(1×a)×6=24,
解得a=8(秒)
b=![]() =2(厘米/秒)
=2(厘米/秒)
(22-8)c=(12×2+6)-2×8
解得c=1(厘米/秒)
故答案为:8;2;1
(3)依题意得:y1=1×8+2(x-8),
即:y1=2x-8(
y2=(30-2×8)-1×(x-8)
=22-x(x>8)
(4)据题意,当y1=y2,P与Q相遇,
即2x-8=(22-x),
解得x=10.
故出发10s时P、Q相遇.

【题目】某公交公司决定更换节能环保的新型公交车![]() 购买的数量和所需费用如下表所示:
购买的数量和所需费用如下表所示:
A型数量 | B型数量 | 所需费用 |
3 | 1 | 450 |
2 | 3 | 650 |
![]() 求A型和B型公交车的单价;
求A型和B型公交车的单价;
![]() 该公司计划购买A型和B型两种公交车共10辆,已知每辆A型公交车年均载客量为60万人次,每辆B型公交车年均载客量为100万人次,若要确保这10辆公交车年均载客量总和不少于670万人次,则A型公交车最多可以购买多少辆?
该公司计划购买A型和B型两种公交车共10辆,已知每辆A型公交车年均载客量为60万人次,每辆B型公交车年均载客量为100万人次,若要确保这10辆公交车年均载客量总和不少于670万人次,则A型公交车最多可以购买多少辆?