题目内容
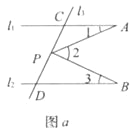
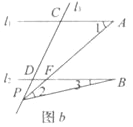
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,给出以下五个结论:①AE=CF;②∠APE=∠CPF;③△EPF是等腰直角三角形;④EF=AP;⑤![]() .当∠EPF在△ABC内绕顶点P旋转时(点E不与点A、B重合),上述结论中始终正确的序号有 .
.当∠EPF在△ABC内绕顶点P旋转时(点E不与点A、B重合),上述结论中始终正确的序号有 .

【答案】①②③⑤
【解析】试题分析:根据等腰直角三角形的性质可得AP⊥BC,AP=PC,∠EAP=∠C=45°,根据同角的余角相等求出∠APE=∠CPF,判定②正确,然后利用“角边角”证明△APE和△CPF全等,根据全等三角形的可得AE=CF,判定①正确,再根据等腰直角三角形的定义得到△EFP是等腰直角三角形,判定③正确;根据等腰直角三角形的斜边等于直角边的![]() 倍表示出EF,可知EF随着点E的变化而变化,判定④错误,根据全等三角形的面积相等可得△APE的面积等于△CPF的面积相等,然后求出四边形AEPF的面积等于△ABC的面积的一半,判定⑤正确.
倍表示出EF,可知EF随着点E的变化而变化,判定④错误,根据全等三角形的面积相等可得△APE的面积等于△CPF的面积相等,然后求出四边形AEPF的面积等于△ABC的面积的一半,判定⑤正确.
试题解析:∵AB=AC,∠BAC=90°,点P是BC的中点,
∴∠EAP=![]() ∠BAC=45°,AP=
∠BAC=45°,AP=![]() BC=CP.
BC=CP.
①在△AEP与△CFP中,
∵∠EAP=∠C=45°,AP=CP,∠APE=∠CPF=90°-∠APF,
∴△AEP≌△CFP,
∴AE=CF.正确;
②由①知,△AEP≌△CFP,
∴∠APE=∠CPF.正确;
③由①知,△AEP≌△CFP,
∴PE=PF.
又∵∠EPF=90°,
∴△EPF是等腰直角三角形.正确;
④只有当F在AC中点时EF=AP,故不能得出EF=AP,错误;
⑤∵△AEP≌△CFP,同理可证△APF≌△BPE.
∴S四边形AEPF=S△AEP+S△APF=S△CPF+S△BPE=![]() S△ABC.正确.
S△ABC.正确.
故正确的序号有①②③⑤

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案【题目】体育老师对九年级(9)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如下所示:
组别 | 次数x | 频数(人数) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 | a |
第4组 | 140≤x<160 | 18 |
第5组 | 160≤x<180 | 6 |

请结合图表完成下列问题:
(1)表中的a=________;
(2)请把频数分布直方图补充完整;
(3)这个样本数据的中位数落在第________组;
(4)若九年级学生一分钟跳绳次数(x)达标要求是:x<120为不合格;120≤x<140,为合格;140≤x<160为良;x≥160为优.根据以上信息,请你给学校或九年级同学提一条合理化建议:_________________________________________________________________.