题目内容
在矩形ABCD中，AB=5，BC=12，⊙A的半径为2，若以C为圆心作一个圆，使⊙C与⊙A相切，那么⊙C的半径为 。
11或15
分析：连接AC，由勾股定理得，圆心距AC=13，再分两圆外切时和两圆内切时，求圆C的半径．
解答：
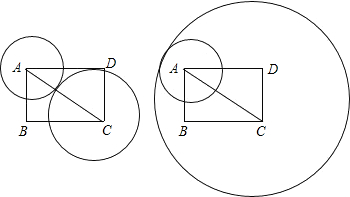
解：连接AC，由勾股定理得，圆心距AC=
=13，∴当两圆外切时，圆C的半径=13-2=11，当两圆内切时，圆C的半径=2+13=15．
点评：本题考查了两圆相切时，两圆的半径与圆心距的关系，注意有两种情况．
练习册系列答案
口算题天天练系列答案
相关题目
所在圆的圆心，∠AOC=108°，点D在AB的延长线上, BD=BC, 则∠D的度数为（ ）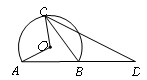
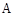，若过点
、点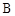
作圆，那么下面说法正确的是（ ）
不在该圆的外部，就在该圆的内部
的中垂线上
则图中三个扇形(阴影部分)的面积之和是 cm2． 
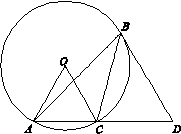
－4
