题目内容
如图 、
、 是
是 的两条弦,
的两条弦, =30°,过点
=30°,过点 的切线与
的切线与 的延长线交于点
的延长线交于点 ,则
,则 的度数为 .
的度数为 .
 、
、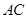 是
是 的两条弦,
的两条弦, =30°,过点
=30°,过点 的切线与
的切线与 的延长线交于点
的延长线交于点 ,则
,则 的度数为 .
的度数为 .
30°
连接OC,则∠OCD=90°,由圆周角定理知,∠COB=2∠A=60°,即可求∠D=90°-∠COB=30°.
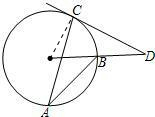
解:连接OC,
∴∠OCD=90°,
∴∠COB=2∠A=60°,
∴∠D=90°-∠COB=30°.
本题利用了切线的概念和圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

解:连接OC,
∴∠OCD=90°,
∴∠COB=2∠A=60°,
∴∠D=90°-∠COB=30°.
本题利用了切线的概念和圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 所在圆的圆心,∠AOC=108°,点D在AB的延长线上, BD=BC, 则∠D的度数为( )
所在圆的圆心,∠AOC=108°,点D在AB的延长线上, BD=BC, 则∠D的度数为( )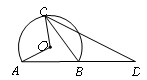
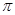
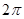 -4
-4 是
是 的外接圆,点
的外接圆,点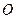
 上,
上,  ,点
,点 是垂足,
是垂足, ,
, .(1)求证:
.(1)求证:
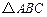 中,AB是
中,AB是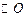 的直径,
的直径,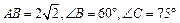 ,
,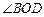 的度数;
的度数;