Question

【题目】如图，E，F是平行四边形ABCD的对角线AC上的点，CE=AF．请你猜想：BE与DF有怎样的位置关系和数量关系？并对你的猜想加以证明：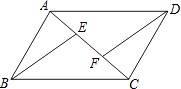

Answer 1

【答案】BE∥DF，BE=DF|连接BD，交AC于点O，连接DE，BF．
∵四边形ABCD是平行四边形，
∴BO=OD，AO=CO，
又∵AF=CE，
∴AE=CF，
∴EO=FO，
∴四边形BEDF是平行四边形，
∴BE∥DF，BE=DF
【解析】答：猜想：BE∥DF，BE=DF．证明：证法一：如图1，
∵四边形ABCD是平行四边形．
∴BC=AD，∠1=∠2，
∵在△BCE和△DAF中，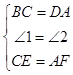
，
∴△BCE≌△DAF（SAS），
∴BE=DF，∠3=∠4，
∴BE∥DF．
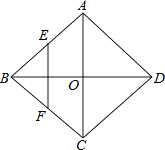
证法二：如图2，
连接BD，交AC于点O，连接DE，BF．
∵四边形ABCD是平行四边形，
∴BO=OD，AO=CO，
又∵AF=CE，
∴AE=CF，
∴EO=FO，
∴四边形BEDF是平行四边形，
∴BE∥DF，BE=DF．
故答案为：BE∥DF，BE=DF；
连接BD，交AC于点O，连接DE，BF．
∵四边形ABCD是平行四边形，
∴BO=OD，AO=CO，
又∵AF=CE，
∴AE=CF，
∴EO=FO，
∴四边形BEDF是平行四边形，
∴BE∥DF，BE=DF．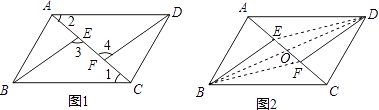

首先连接BD，交AC于点O，连接DE，BF．由四边形ABCD是平行四边形，可得BO=OD，AO=CO，又由CE=AF，可得OE=OF，即可证得四边形BEDF是平行四边形，则可得BE∥DF，BE=DF