题目内容
【题目】在矩形ABCD中，AD=2AB=4，E是AD的中点，一块足够大的三角板的直角顶点与点E重合，将三角板绕点E旋转，三角板的两直角边分别交AB，BC（或它们的延长线）于点M，N，设∠AEM=α（0°＜α＜90°），给出下列四个结论： ①AM=CN；
②∠AME=∠BNE；
③BN﹣AM=2；
④S△EMN= 
．
上述结论中正确的个数是（ ）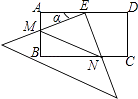
A.1
B.2
C.3
D.4
【答案】C
【解析】解：①如图， 
在矩形ABCD中，AD=2AB，E是AD的中点，
作EF⊥BC于点F，则有AB=AE=EF=FC，
∵∠AEM+∠DEN=90°，∠FEN+∠DEN=90°，
∴∠AEM=∠FEN，
在Rt△AME和Rt△FNE中，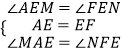
，
∴Rt△AME≌Rt△FNE，
∴AM=FN，
∴MB=CN．
∵AM不一定等于CN，
∴①错误，
②由①有Rt△AME≌Rt△FNE，
∴∠AME=∠BNE，
∴②正确，
③由①得，BM=CN，
∵AD=2AB=4，
∴BC=4，AB=2
∴BN﹣AM=BC﹣CN﹣AM=BC﹣BM﹣AM=BC﹣（BM+AM）=BC﹣AB=4﹣2=2，
∴③正确，
④方法一：如图，
由①得，CN=CF﹣FN=2﹣AM，AE= 
AD=2，AM=FN
∵tanα= 
，
∴AM=AEtanα
∵cosα= 
= 
，
∴cos2α= ，
∴ 
=1+ 
=1+（ ）2=1+tan2α，
∴ 
=2（1+tan2α）
∴S△EMN=S四边形ABNE﹣S△AME﹣S△MBN
= （AE+BN）×AB﹣ AE×AM﹣ BN×BM
= （AE+BC﹣CN）×2﹣ AE×AM﹣ （BC﹣CN）×CN
= （AE+BC﹣CF+FN）×2﹣ AE×AM﹣ （BC﹣2+AM）（2﹣AM）
=AE+BC﹣CF+AM﹣ AE×AM﹣ （2+AM）（2﹣AM）
=AE+AM﹣ AE×AM+ AM2
=AE+AEtanα﹣ AE2tanα+ AE2tan2α
=2+2tanα﹣2tanα+2tan2α
=2（1+tan2α）
= ．
方法二，∵E是AD的中点，
∴AE= AD=2，
在Rt△AEM，cosα= 
，
∴EM= 
= 
，
由（1）知，Rt△AME≌Rt△FNE，
∴EM=EN，∠AEM=∠FEN，
∵∠AEF=90°，
∴∠MEN=90°，
∴△MEN是等腰直角三角形，
∴S△MEN= EM2= ．
∴④正确．
故选C．
【考点精析】掌握旋转的性质是解答本题的根本，需要知道①旋转后对应的线段长短不变，旋转角度大小不变；②旋转后对应的点到旋转到旋转中心的距离不变；③旋转后物体或图形不变，只是位置变了．
