Question

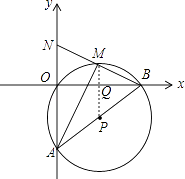
【题目】如图，在平面直角坐标系中，O（0，0），A（0，﹣6），B（8，0）三点在⊙P上．

（1）求圆的半径及圆心P的坐标；
（2）M为劣弧 的中点，求证：AM是∠OAB的平分线；
（3）连接BM并延长交y轴于点N，求N，M点的坐标．

Answer 1

【答案】
（1）解：∵O（0，0），A（0，﹣6），B（8，0），

∴OA=6，OB=8，

∴AB= =10，

∵∠AOB=90°，

∴AB为⊙P的直径，

∴⊙P的半径是5

∵点P为AB的中点，

∴P（4，﹣3）

（2）解：∵M点是劣弧OB的中点，

∴ = ，

∴∠OAM=∠MAB，

∴AM为∠OAB的平分线

（3）解：连接PM交OB于点Q，如图，

∵ = ，

∴PM⊥OB，BQ=OQ= OB=4，

在Rt△PBQ中，PQ= = =3，

∴MQ=2，

∴M点的坐标为（4，2）；

∵MQ∥ON，

而OQ=BQ，

∴MQ为△BON的中位线，

∴ON=2MQ=4，

∴N点的坐标为（0，4）．

【解析】本题考查了圆的综合题：熟练掌握垂径定理和圆周角定理；理解坐标与图形的性质，记住线段的中点坐标公式，会利用勾股定理计算线段的长．此类题目通常解由半径、弦心距和弦的一半所组成的直角三角形．（1）先利用勾股定理计算出AB=10，再利用圆周角定理的推理可判断AB为⊙P的直径，则得到⊙P的半径是5，然后利用线段的中点坐标公式得到P点坐标；（2）根据圆周角定理由 = ，∠OAM=∠MAB，于是可判断AM为∠OAB的平分线；（3）连接PM交OB于点Q，如图，先利用垂径定理的推论得到PM⊥OB，BQ=OQ= OB=4，再利用勾股定理计算出PQ=3，则MQ=2，于是可写出M点坐标，接着证明MQ为△BON的中位线得到ON=2MQ=4，然后写出N点的坐标．