Question

【题目】如图，在直角梯形ABCD中，AD∥BC，∠C＝90°，AD＝5，BC＝9，以A为中心将腰AB顺时针旋转90°至AE，连接DE，则△ADE的面积等于 （ ）

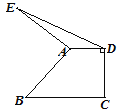
A．10 B．11 C．12 D．13

Answer 1

【答案】A

【解析】

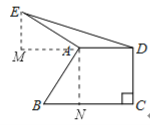
试题分析：过A作AN⊥BC于N，将△BNA绕着点A顺时针旋转90°至△EAM的位置，则△EAM≌△BNA，所以∠EAM=∠NAB，EM=BN，因为∠EAM+∠BAM=90°，所以∠MAB+∠NAB=90°，又因为∠DAN=90°，所以点MAD在同一条直线上，所以EM是△ADE边AD上的高，因为在直角梯形ABCD中，AD∥BC，∠C＝90°，AD＝5，BC＝9，AN⊥BC，所以AD=NC=5，所以EM=BN=4，所以△ADE的面积是×AD×EM=×5×4=10，故选：A．