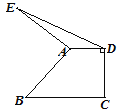
题目内容
【题目】如图,从下列三个条件中:(1)![]() ; (2)
; (2)![]() ; (3)
; (3)![]() .任选两个作为条件,另一个作为结论,书写出一个真命题,并证明.
.任选两个作为条件,另一个作为结论,书写出一个真命题,并证明.

命题:
证明:
【答案】见解析.
【解析】分析:根据题意可知已知AD∥CB,AB∥CD求证∠A=∠C.欲证∠A=∠C,需证明∠A=∠ABF且∠C=∠ABF,根据两直线平行,内错角相等及两直线平行,同位角相等可证.
本题解析:
命题:如果 AD∥CB, AB∥CD ,那么∠A=∠C(答案不唯一)
证明:∵AD∥CB
∴∠A=∠ABF
∵AB∥CD
∴∠C=∠ABF
又∵ ∠A=∠ABF
∴∠A=∠C
点睛: 此题考查了平行线的判定与性质,解答此类判定两角相等的问题,需先确定两角的位置关系,由平行线的性质求出两角相等即可.本题是一道探索性条件开放性题目,能有效地培养“执果索因”的思维方式与能力.

练习册系列答案
相关题目