题目内容
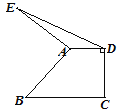
【题目】如图,点![]() 为⊙
为⊙![]() 上一点,点
上一点,点![]() 在直径
在直径![]() 的延长线上,且
的延长线上,且![]() .
.
(1)判断直线![]() 和⊙
和⊙![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
(2)过点![]() 作⊙
作⊙![]() 的切线
的切线![]() 交直线
交直线![]() 于点
于点![]() ,若
,若![]() ,⊙
,⊙![]() 的半径是
的半径是![]() ,求
,求![]() 的长.
的长.

【答案】(1)直线CD和⊙O的位置关系是相切,理由见解析;(2)6.
【解析】试题分析:(1)连接OD,根据圆周角定理求出∠DAB+∠DBA=90°,求出∠CDA+∠ADO=90°,根据切线的判定推出即可;
(2)根据勾股定理求出DC,根据切线长定理求出DE=EB,根据勾股定理得出方程,求出方程的解即可.
试题解析:(1)直线CD和⊙O的位置关系是相切,
理由是:连接OD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠DBA=90°,
∵∠CDA=∠CBD,
∴∠DAB+∠CDA=90°,
∵OD=OA,
∴∠DAB=∠ADO,
∴∠CDA+∠ADO=90°,
即OD⊥CE,
已知D为⊙O的一点,
∴直线CD是⊙O的切线,
即直线CD和⊙O的位置关系是相切;
(2)∵AC=2,⊙O的半径是3,
∴OC=2+3=5,OD=3,
在Rt△CDO中,由勾股定理得:CD=4,
∵CE切⊙O于D,EB切⊙O于B,
∴DE=EB,∠CBE=90°,
设DE=EB=x,
在Rt△CBE中,由勾股定理得:CE2=BE2+BC2,
则(4+x)2=x2+(5+3)2,
解得:x=6,
即BE=6.


 阅读快车系列答案
阅读快车系列答案【题目】泉州市某校准备组织教师、学生、家长到福州进行参观学习活动,旅行社代办购买动车票,动车票价格如下表所示:
运行区间 | 大人票价 | 学生票 | ||
出发站 | 终点站 | 一等座 | 二等座 | 二等座 |
泉州 | 福州 | 61.5(元) | 50.5(元) | 38(元) |
根据报名总人数,若所有人员都买一等座的动车票,则共需13530元,若都买二等座动车票(学生全部按表中的“学生票二等座”购买),则共需8860元;已知家长的人数是教师的人数的3倍。
(1)报名参加活动的总人数为___________人;
(2)求参加活动的教师与学生的人数;
(3)如果买到a张成人二等座票,且学生全部按表中的“学生票二等座”购买,其余的买一等座票,但个别家长因临时不参加活动退票,退票人数刚好是所买一等座票数的![]() ,已知退票的是一等座票,退票收取票价10%的退票费,最终买票的总费用为8859.3元,求a的值。
,已知退票的是一等座票,退票收取票价10%的退票费,最终买票的总费用为8859.3元,求a的值。