题目内容
【题目】已知直线y=kx+b与抛物线y=ax2(a>0)相交于A、B两点(点A在点B的左侧),与y轴正半轴相交于点C,过点A作AD⊥x轴,垂足为D.
(1)若∠AOB=60°,AB∥x轴,AB=2,求a的值;
(2)若∠AOB=90°,点A的横坐标为﹣4,AC=4BC,求点B的坐标;
(3)延长AD、BO相交于点E,求证:DE=CO.

【答案】(1)![]() ;(2)B(1,
;(2)B(1, ![]() );(3)证明见解析.
);(3)证明见解析.
【解析】试题分析:(1)如图1,由条件可知△AOB为等边三角形,则可求得OA的长,在Rt△AOD中可求得AD和OD的长,可求得A点坐标,代入抛物线解析式可得a的值;
(2)如图2,作辅助线,构建平行线和相似三角形,根据CF∥BG,由A的横坐标为-4,得B的横坐标为1,所以A(-4,16a),B(1,a),证明△ADO∽△OEB,则![]() ,得a的值及B的坐标;
,得a的值及B的坐标;
(3)如图3,设AC=nBC由(2)同理可知:A的横坐标是B的横坐标的n倍,则设B(m,am2),则A(-mn,am2n2),分别根据两三角形相似计算DE和CO的长即可得出结论.
试题解析:(1)如图1,
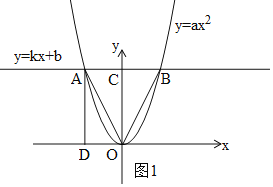
∵抛物线y=ax2的对称轴是y轴,且AB∥x轴,
∴A与B是对称点,O是抛物线的顶点,
∴OA=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∵AB=2,AB⊥OC,
∴AC=BC=1,∠BOC=30°,
∴OC=![]() ,
,
∴A(-1, ![]() ),
),
把A(-1, ![]() )代入抛物线y=ax2(a>0)中得:a=
)代入抛物线y=ax2(a>0)中得:a=![]() ;
;
(2)如图2,过B作BE⊥x轴于E,过A作AG⊥BE,交BE延长线于点G,交y轴于F,
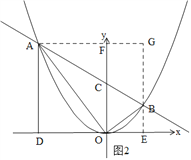
∵CF∥BG,
∴![]() ,
,
∵AC=4BC,
∴![]() =4,
=4,
∴AF=4FG,
∵A的横坐标为-4,
∴B的横坐标为1,
∴A(-4,16a),B(1,a),
∵∠AOB=90°,
∴∠AOD+∠BOE=90°,
∵∠AOD+∠DAO=90°,
∴∠BOE=∠DAO,
∵∠ADO=∠OEB=90°,
∴△ADO∽△OEB,
∴![]() ,
,
∴![]() ,
,
∴16a2=4,
a=±![]() ,
,
∵a>0,
∴a=![]() ;
;
∴B(1, ![]() );
);
(3)如图3,
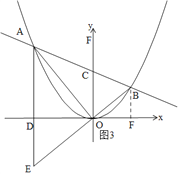
设AC=nBC,
由(2)同理可知:A的横坐标是B的横坐标的n倍,
则设B(m,am2),则A(-mn,am2n2),
∴AD=am2n2,
过B作BF⊥x轴于F,
∴DE∥BF,
∴△BOF∽△EOD,
∴![]() ,
,
∴![]() ,
,
∴![]() ,DE=am2n,
,DE=am2n,
∴![]() ,
,
∵OC∥AE,
∴△BCO∽△BAE,
∴![]() ,
,
∴![]() ,
,
∴CO=![]() =am2n,
=am2n,
∴DE=CO.

 天天练口算系列答案
天天练口算系列答案