题目内容
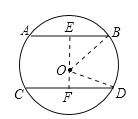
【题目】如图,已知⊙O的半径长为R=5,弦AB 与弦CD平行,他们之间距离为7,AB=6求:弦CD的长.

【答案】8.
【解析】试题分析:如图1所示:过O作OE⊥AB,交CD于F点,连接OB,OD,可得出OB=OD=5,在直角三角形OBE中,利用勾股定理求出OE的长,从而得到OF的长,在直角三角形ODF中,利用勾股定理分别求出FD,即可得到结论.
试题解析:解: 过O向AB作垂线,垂足为E,根据垂径定理可以得到BE=3,连接OB,
在直角三角形BOE中,根据勾股定理可以得到OE= ![]() =4.
=4.
同样过O点想CD作垂线,垂足为F,
因为弦AB和弦CD之间的距离为7,
那么OF=3,
连接OD,在直角三角形ODF中DF= ![]() =4.
=4.
根据垂径定理可以知道点F为CD的中点,即CD=8.

练习册系列答案
相关题目
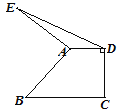
【题目】如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AD=5,BC=9,以A为中心将腰AB顺时针旋转90°至AE,连接DE,则△ADE的面积等于 ( )
A.10 B.11 C.12 D.13


