��Ŀ����
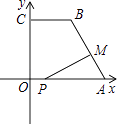
����Ŀ����ͼ��������y=ax2+bx+c��a��0���Ķ���ΪM��ֱ��y=m��x��ƽ�У����������߽��ڵ�A��B������AMBΪ����ֱ�������Σ����ǰ���������A��B����֮��IJ������߶�ABΧ�ɵ�ͼ�γ�Ϊ�������߶�Ӧ�����Σ��߶�AB��Ϊ����������M��Ϊ��������M���߶�AB�ľ���Ϊ���ߣ�
��1��������y=x2��Ӧ�ĵ���Ϊ��������y= ![]() x2��Ӧ�ĵ���Ϊ��������y=ax2��a��0����Ӧ�ĵ���Ϊ��������y=a��x��3��2+2��a��0����Ӧ�ĵ���Ϊ��
x2��Ӧ�ĵ���Ϊ��������y=ax2��a��0����Ӧ�ĵ���Ϊ��������y=a��x��3��2+2��a��0����Ӧ�ĵ���Ϊ��
��2������ͼ��1���еĽ��ۣ�������y=ax2��4ax�� ![]() ��a��0����Ӧ�ĵ���Ϊ6���������ߵĽ���ʽ��
��a��0����Ӧ�ĵ���Ϊ6���������ߵĽ���ʽ��
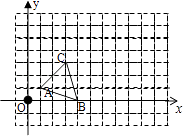
��3����������yn=anx2+bnx+cn��an��0���Ķ�Ӧ���μ�ΪFn��n=1��2��3������������F1 �� F2 �� ��..FnΪ�������Σ���Ӧ�ĵ���֮�ȼ�Ϊ���Ʊȣ���Fn��Fn��1�����Ʊ�Ϊ ![]() ����Fn�ĵ�����Fn��1�ĵ������е㣬���ڽ���2������õ�������Ϊy1 �� ���Ӧ�����μ�ΪF1 ��
����Fn�ĵ�����Fn��1�ĵ������е㣬���ڽ���2������õ�������Ϊy1 �� ���Ӧ�����μ�ΪF1 ��
����������y2�ı���ʽ��
����F1�ĵ���Ϊh1 �� F2�ĵ���Ϊh2 �� ��Fn�ĵ���Ϊhn �� ��hn= �� Fn�ĵ����Ҷ˵������Ϊ �� 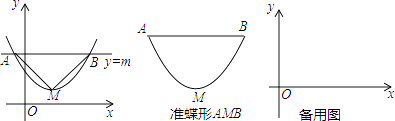
���𰸡�
��1��2��4��![]() ��
��![]()
��2��
�⣺�ɣ�1����֪����Ϊ ![]() =6��
=6��
��a= ![]() ��
��
�������ߵĽ���ʽΪy= ![]() x2��
x2�� ![]() x��
x�� ![]()
��3��![]() ��3+
��3+ ![]()
���������⣺��1�����ݵ����Ķ����Լ�����ֱ�������ε����ʿ��Լ���B��m��m�����ٰ�B��m��m������y=x2 �� �õ�m=1��0����������
��A����1��1����B��1��1����
��AB=2��������Ϊ2���ڰ�B��m��m������y= ![]() x2 �� �õ�m=2��0����������
x2 �� �õ�m=2��0����������
��A����2��2����B��2��2����
��AB=4��������Ϊ4���۰�B��m��m������y=ax2 �� �õ�m= ![]() ��0����������
��0����������
��A���� ![]() ��
�� ![]() ����B��
����B�� ![]() ��
�� ![]() ����
����
��AB= ![]() ��������Ϊ
��������Ϊ ![]() ���ܸ��ݵ����Ķ����Լ�����ֱ�������ε����ʣ������Ĵ�С�붥���λ���أ�����
���ܸ��ݵ����Ķ����Լ�����ֱ�������ε����ʣ������Ĵ�С�붥���λ���أ����� ![]() ��
��
�ʴ𰸷ֱ�Ϊ2��4�� ![]() ��
�� ![]() ����3���١�y1=
����3���١�y1= ![]() x2��
x2�� ![]() x��
x�� ![]() =
= ![]() ��x��2��2��3�ĵ���AB��x���ϣ���A��B��ߣ���
��x��2��2��3�ĵ���AB��x���ϣ���A��B��ߣ���
��A����1��0����B��5��0����
��������y2�Ķ�������Ϊ��2��0����
��F2�ĵ�����F1�ĵ���=1��2��
�� ![]() ��
�� ![]() =1��2��
=1��2��
��a1= ![]() ��
��
��a2= ![]() ��
��
��������y2�Ľ���ʽΪy= ![]() ��x��2��2 �� �ڡ�hn��hn��1=1��2��h1=3��
��x��2��2 �� �ڡ�hn��hn��1=1��2��h1=3��
��h2= ![]() ��h3=
��h3= ![]() ��h4=
��h4= ![]() ������hn=
������hn= ![]() ��
��
������Ҷ˵�B�� �����꣬B1�ĺ�����3��B2�ĺ�����Ϊ3+ ![]() ��B3�ĺ�����Ϊ3+
��B3�ĺ�����Ϊ3+ ![]() ��B4�ĺ�����Ϊ3+
��B4�ĺ�����Ϊ3+ ![]() ����Bn�ĺ�����Ϊ3+
����Bn�ĺ�����Ϊ3+ ![]() ��
��
���Դ��� ![]() ��3+
��3+ ![]() ��
��
�����㾫�����������⣬������Ҫ�˽���κ����ĸ���(һ��أ��Ա���x�������y֮��������¹�ϵ��һ��ʽ��y=ax2+bx+c(a��0��a��b��cΪ����)�����yΪx�Ķ��κ���)����Ҫ���ն��κ�����ͼ��(���κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ��)�����֪ʶ���Ǵ���Ĺؼ���

����Ŀ������y=x2+3x+2��ͼ����ͼ1��ʾ������ͼ��ش����⣺ 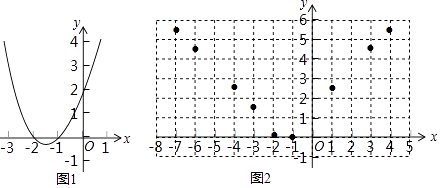
��1����xʱ��x2+3x+2��0��
��2������������Ļ����ϣ�̽����������⣺ �ٺ���y= ![]() ���Ա���x��ȡֵ��Χ����
���Ա���x��ȡֵ��Χ����
������Ǻ���y= ![]() �ļ���y��x�Ķ�Ӧֵ��
�ļ���y��x�Ķ�Ӧֵ��
x | �� | ��7 | ��6 | ��4 | ��3 | ��2 | ��1 | 0 | 1 | 3 | 4 | �� |
y | �� | 5.477�� | 4.472�� | 2.449�� | 1.414�� | 0 | 0 | 1.414�� | 2.449�� | 4.472�� | 5.477�� | �� |
��ͼ2����ƽ��ֱ������ϵxOy�У�������ϱ��и��Զ�ӦֵΪ����ĵ�Ĵ��λ�ã������������ĵ㣬�����ú�����ͼ��
��д���ú�����һ�����ʣ� ��
����Ŀ��Ϊ����ѧ������ѧϰϰ�ߣ�ijѧУ�ƻ�����һ�Ρ��������⼯����չʾ����Ը�У����ѧ�����������⼯�������������һ�γ������飬�����ռ������ݻ��������治������ͳ��ͼ���������ͼ�����ṩ����Ϣ������������⣺
������� | Ƶ�� | Ƶ�� |
�dz��� | 0.21 | |
�Ϻ� | 70 | |
һ�� | ||
���� | 36 |
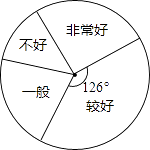
��1�����γ����������˶���ѧ����
��2����ȫͳ�Ʊ�����ȱ�����ݣ�
��3����У��1500��ѧ�������Ƹ�Уѧ���������⼯������dz��á��͡��Ϻá���ѧ��һ��Լ��������
��4��ijѧϰС��4��ѧ���Ĵ��⼯�У���2�����dz��á�����ΪA1��A2����1�����Ϻá�����ΪB����1����һ�㡱����ΪC������Щ���⼯������������������״����С����ɫ�����������ȫ��ͬ�����г�ȡһ�������Żأ������µ�3�����⼯���ٳ�ȡһ�������á��б�����������ͼ���ķ���������γ鵽�Ĵ��⼯���ǡ��dz��á��ĸ��ʣ�