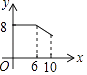��Ŀ����
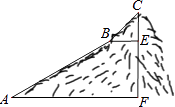
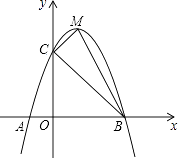
����Ŀ����ͼ����֪A��B���������ֱ�Ϊ��40��0���ͣ�0��30��������P�ӵ�A��ʼ���߶�AO����ÿ��2�����ȵ�λ���ٶ���ԭ��O�˶�����ֱ��EF��x�Ὺʼ��ÿ1����λ���ٶ�����ƽ���ƶ�����EF��x�ᣩ�����ҷֱ���y�ᡢ�߶�AB���ڵ�E��F������EP��FP���趯��P�붯ֱ��EFͬʱ�������˶�ʱ��Ϊt�룮 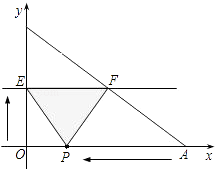
��1����t=15ʱ����PEF�������
��2��ֱ��EF����P���˶������У��Ƿ����������t��ʹ�á�PEF���������160��ƽ����λ���������ڣ��������ʱt��ֵ���������ڣ���˵�����ɣ�
��3����tΪ��ֵʱ����EOP���BOA���ƣ�
���𰸡�
��1���⣺��EF��OA��
���BEF=��BOA
�֡ߡ�B=��B��
���BEF�ס�BOA��
�� ![]()
��t=15ʱ��OE=BE=15��OA=40��OB=30��
�� ![]()
��S��PEF= ![]() EFOE=
EFOE= ![]() ��ƽ����λ��
��ƽ����λ��
��2���⣺�ߡ�BEF�ס�BOA��
�� ![]()
�� ![]()
��������t2��30t+240=0
�ߡ�=302��4��1��240=��60��0�����û��ʵ������
�����ʹ�á�PEF���������160��ƽ����λ����tֵ
��3���⣺����EPO=��BAOʱ����EOP�ס�BOA
�� ![]() ����
���� ![]()
��ã�t=12��11�֣�
����EPO=��ABOʱ����EOP�ס�AOB
�� ![]() ����
���� ![]()
��ã� ![]()
�൱t=12�� ![]() ʱ����EOP�ס�BOA
ʱ����EOP�ס�BOA
����������1������EF��x�ᣬ��S��PEF= ![]() EFOE��t=15ʱ��OE=15���ؼ�����EF����֤��BEF�ס�BOA����
EFOE��t=15ʱ��OE=15���ؼ�����EF����֤��BEF�ס�BOA���� ![]() ���Ӷ����EF�ij��ȣ��ó���PEF���������2���������������t��ʹ�á�PEF���������160������������ʽ�г����̣��ɸ����б�ʽ�����жϣ��ó����ۣ���3�������EOP���BOA���ƣ����ڡ�EOP=��BOA=90�㣬��ֻ�ܵ�O���O��Ӧ��Ȼ�����������ֱ����ۣ��ٵ�P���A��Ӧ���ڵ�P���B��Ӧ��
���Ӷ����EF�ij��ȣ��ó���PEF���������2���������������t��ʹ�á�PEF���������160������������ʽ�г����̣��ɸ����б�ʽ�����жϣ��ó����ۣ���3�������EOP���BOA���ƣ����ڡ�EOP=��BOA=90�㣬��ֻ�ܵ�O���O��Ӧ��Ȼ�����������ֱ����ۣ��ٵ�P���A��Ӧ���ڵ�P���B��Ӧ��
�����㾫����������Ŀ����֪���������������ʽ�����������ε��ж������ʵ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���ո����б�ʽ��=b2-4ac��������Է�Ϊ3�������1������>0ʱ��һԪ���η�����2������ȵ�ʵ����2������=0ʱ��һԪ���η�����2����ͬ��ʵ����3������<0ʱ��һԪ���η���û��ʵ���������������ε�һ�ж�Ӧ�߶�(��Ӧ�ߡ���Ӧ���ߡ���Ӧ��ƽ���ߡ����Բ�뾶������Բ�뾶�ȣ��ıȵ������Ʊȣ������������ܳ��ıȵ������Ʊȣ���������������ıȵ������Ʊȵ�ƽ����