题目内容
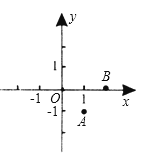
【题目】如图，一次函数与反比例函数y= 
的图象交于A（1，4），B（4，n）两点． 
（1）求反比例函数的解析式；
（2）点P是x轴上的一动点，试确定点P使PA+PB最小，并求出点P的坐标．
【答案】
（1）解：将A（1，4）代入y= 
，
∴m=4，
∴反比例函数的解析式为：y= 
（2）解：将B（4，n）代入y= ，
∴n=1，
设C与A关于x轴对称，
∴C（1，﹣4），
设直线BC的解析式为：y=kx+b，
将C（1，﹣4）和B（4，1）代入y=kx+b，
∴解得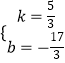 
∴一次函数的解析式为：y= 
x﹣ 
令y=0代入y= x﹣
∴x= 
∴P（ ，0）
【解析】（1）将A代入反比例函数即可求出m的值．（2）将B代入反比例函数即可求出n的值，求出点A的关于x轴的对称点坐标C，然后将BC的解析式求出，令y=0代入AC的解析式即可求出P的坐标．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
