题目内容
如图所示，AB=AC，AB为⊙O的直径，AC、BC分别交⊙O于E、D，连接ED、BE．
（1）试判断DE与BD是否相等，并说明理由；
（2）如果BC=6，AB=5，求BE的长．
（1）试判断DE与BD是否相等，并说明理由；
（2）如果BC=6，AB=5，求BE的长．
（1）DE=BD
证明：连接AD，则AD⊥BC，
在等腰三角形ABC中，AD⊥BC，
∴∠CAD=∠BAD（等腰三角形三线合一），
∴
=
，
∴DE=BD；
（2）∵AB=5，BD=
BC=3，
∴AD=4，
∵AB=AC=5，
∴AC•BE=CB•AD，
∴BE=4.8．
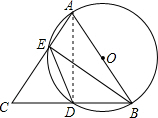
证明：连接AD，则AD⊥BC，
在等腰三角形ABC中，AD⊥BC，
∴∠CAD=∠BAD（等腰三角形三线合一），
∴
 |
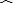| ED |
|
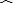| BD |
∴DE=BD；
（2）∵AB=5，BD=
| 1 |
| 2 |
∴AD=4，
∵AB=AC=5，
∴AC•BE=CB•AD，
∴BE=4.8．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
