��Ŀ����
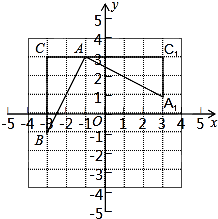
����Ŀ����ͼ��������y=ax2��5ax��6a��x����A��B���㣨A��B�ң�����y���ڵ�C��ֱ��y=��x+b����������D����x����E���ҡ�ACE�����Ϊ6��
��1���������ߵĽ���ʽ��
��2����PΪCD�Ϸ���������һ�㣬����P��x���ƽ���ߣ���ֱ��CD��F����P��ĺ�����Ϊm���߶�PF�ij�Ϊd����d��m�ĺ�����ϵʽ��
��3���ڣ�2���������£�����P��PG��CD������ΪG������APG=��ACO�����P�����꣮
���𰸡�
��1��
�⣺��y=0����y=ax2��5ax��6a�ã�ax2��5ax��6a=0��
��a��x��6����x+1��=0��
��x=6��x=��1��
��A����1��0����B��6��0��
��y=0����y=��x+b�ã���x+b=0����ã�x=b����x=0����y=x+b�ã�y=b��
��OC=b��AE=b+1��
��S��ACE= ![]() b��b+1��=6��
b��b+1��=6��
��ã�b=3��b=��4����ȥ����
��C��0��3����
����C��������������ߵĽ���ʽ�ã���6a=3�����a=�� ![]() ��
��
�������ߵĽ���ʽΪy=�� ![]() x2+
x2+ ![]() x+3��
x+3��
��2��
�⣺��b=3��
��ֱ��CE�Ľ���ʽΪy=��x+3��
��P��m���� ![]() m2+
m2+ ![]() m+3����
m+3����
��PF��x�ᣬ
���F���������� ![]() m2+
m2+ ![]() m+3��
m+3��
�ੁx+3=�� ![]() m2+
m2+ ![]() m+3��
m+3��
��x= ![]() m2��
m2�� ![]() m��
m��
��d=PF=m���� ![]() m2��
m2�� ![]() m��=��
m��=�� ![]() m2+
m2+ ![]() m��
m��
��3��
�⣺��ͼ1��ʾ��
��OA=1��OC=3��
��tan��ACO= ![]() ��
��
�ߡ�APG=��ACO��
��tan��APG= ![]() ��
��
��ͼ1��ʾ������P��PC��x�ᣬ����ΪN������A��AM��PG������ΪM��

��OC=OE����COE=90�㣬
���CEO=45�㣮
�֡ߡ�EGH=90�㣬
���GHO=45�㣮
���AMHΪ����ֱ�������Σ�
��MH=AM=a��
��AH= ![]() a��PH=4a��
a��PH=4a��
��Rt��PHN��PN=AN=2 ![]() a��
a��
��AN= ![]() a��
a��
��tan��PAN=2��
��P��m���� ![]() m2+
m2+ ![]() m+3������PN=��
m+3������PN=�� ![]() m2+
m2+ ![]() m+3��AN=m+1����
m+3��AN=m+1���� ![]() =2��
=2��
��ã�m=��1����ȥ����m=2��
��P��2��6����
��ͼ2��ʾ������P��PC��x�ᣬ����ΪN������A��AM��PG������ΪM��

��AM=a����MP=3a��
��OC=OE����COE=90�㣬
���CEO=45�㣮
�֡ߡ�EGH=90�㣬
���GHO=45�㣮
���AMHΪ����ֱ�������Σ�
��MH=AM=a��
��AH= ![]() a��PH=2a��
a��PH=2a��
��Rt��PHN��PN=AN= ![]() a��
a��
��AN=2 ![]() a��
a��
��tan��PAN= ![]() ��
��
�� ![]() =
= ![]() ����ã�m=��1��m=5��
����ã�m=��1��m=5��
��P��5��3����
������������P������ΪP��2��6����P��5��3����
����������1����y=0���������ߵĽ���ʽ����÷��̵Ľ⣬�Ӷ��ɵõ���A�͵�B�����꣬Ȼ�����ݡ�ACE�����Ϊ6�����b��ֵ��Ȼ��ɵõ���C�����꣬�ʴ˿ɵõ�a��ֵ����2��ֱ��CE�Ľ���ʽΪy=��x+3����P��m���� ![]() m2+
m2+ ![]() m+3����Ȼ�����õ�F�ĺ����꣬�������d=PF�ɵõ�d��m�ĺ�����ϵʽ����3������P��PC��x�ᣬ����ΪN������A��AM��PG������ΪM��Ȼ��֤����AMH�͡�PHN��Ϊ����ֱ�������Σ���MH=AM=a��Ȼ������PN��AN�ij����ʴ˿ɵõ�tan��PAN=2��tan��PAN=
m+3����Ȼ�����õ�F�ĺ����꣬�������d=PF�ɵõ�d��m�ĺ�����ϵʽ����3������P��PC��x�ᣬ����ΪN������A��AM��PG������ΪM��Ȼ��֤����AMH�͡�PHN��Ϊ����ֱ�������Σ���MH=AM=a��Ȼ������PN��AN�ij����ʴ˿ɵõ�tan��PAN=2��tan��PAN= ![]() ��Ȼ���г�����m�ķ�����⼴�ɣ�
��Ȼ���г�����m�ķ�����⼴�ɣ�
�����㾫�����������⣬������Ҫ�˽����ֱ��������(����ֱ��������������ֱ�DZ���ȵ�ֱ�������Σ�����ֱ�������ε�����������ҵ���45��)����Ҫ����������Ǻ����Ķ���(���A�����ҡ����ҡ����С����ж�������A��������Ǻ���)�����֪ʶ���Ǵ���Ĺؼ���

 ����Ӣ��ϵ�д�
����Ӣ��ϵ�д�