题目内容
【题目】某电子厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=﹣2x+100.(利润=售价﹣制造成本)
(1)写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月能获得350万元的利润?当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?
(3)根据相关部门规定,这种电子产品的销售单价不能高于32元,如果厂商要获得每月不低于350万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元?
【答案】
(1)解:z=(x﹣18)y=(x﹣18)(﹣2x+100)=﹣2x2+136x﹣1800,
∴z与x之间的函数解析式为z=﹣2x2+136x﹣1800;
(2)解:由z=350,得350=﹣2x2+136x﹣1800,
解这个方程得x1=25,x2=43,
所以,销售单价定为25元或43元,
将z═﹣2x2+136x﹣1800配方,得z=﹣2(x﹣34)2+512,
因此,当销售单价为34元时,每月能获得最大利润,最大利润是512万元;
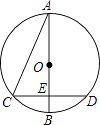
(3)解:结合(2)及函数z=﹣2x2+136x﹣1800的图象(如图所示)可知,
当25≤x≤43时z≥350,
又由限价32元,得25≤x≤32,
根据一次函数的性质,得y=﹣2x+100中y随x的增大而减小,
∴当x=32时,每月制造成本最低.最低成本是18×(﹣2×32+100)=648(万元),
因此,所求每月最低制造成本为648万元.

【解析】(1)根据每月的利润z=(x﹣18)y,再把y=﹣2x+100代入即可求出z与x之间的函数解析式,(2)把z=350代入z=﹣2x2+136x﹣1800,解这个方程即可,把函数关系式变形为顶点式运用二次函数的性质求出最值;(3)根据销售单价不能高于32元,厂商要获得每月不低于350万元的利润得出销售单价的取值范围,进而解决问题.

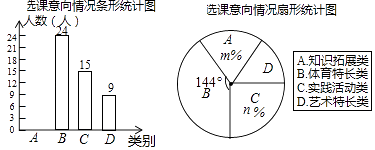
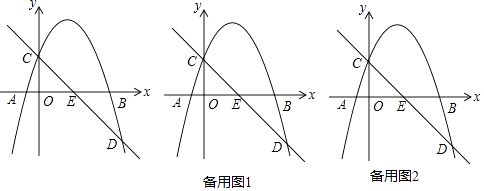
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表: 请结合图表完成下列各题:
组别 | 成绩x分 | 频数(人数) |
第1组 | 50≤x<60 | 6 |
第2组 | 60≤x<70 | 8 |
第3组 | 70≤x<80 | 14 |
第4组 | 80≤x<90 | a |
第5组 | 90≤x<100 | 10 |

(1)表中a的值为;
(2)频数分布直方图补充完整;
(3)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?