题目内容
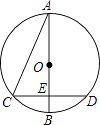
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连接DE、OE. 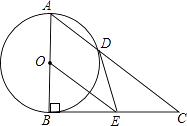
(1)求证:DE与⊙O相切;
(2)求证:BC2=2CDOE;
(3)若cosC= ![]() ,DE=4,求AD的长.
,DE=4,求AD的长.
【答案】
(1)证明:如图1,

连接BD,OD,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠BDC=90°,
在Rt△BDC中,E是BC的中点,
∴DE=CE=BE= ![]() BC,
BC,
∴∠3=∠4,
∵OD=OB,
∴∠1=∠2,
∴∠ODE=∠1+∠3=∠2+∠4=90°,
∴DE与⊙O相切
(2)证明:如图2,
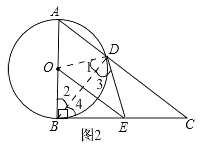
在直角三角形ABC中,∠C+∠A=90°,
在直角三角形BDC中,∠C+∠4=90°,
∴∠A=∠4,
又∵∠C=∠C,
∴△BCD∽△ACB,
![]() ,
,
∴BC2=ACCD,
∵O是AB的中点,E是BC的中点,
∴AC=2OE,
∴BC2=2CDOE
(3)解:如图3,

由(2)知,DE= ![]() BC,又DE=4,
BC,又DE=4,
∴BC=8,
在直角三角形BDC中, ![]() =cosC=
=cosC= ![]() ,
,
∴CD= ![]() ,
,
在直角三角形ABC中, ![]() =cosC=
=cosC= ![]() ,
,
∴AC=12,
∴AD=AC﹣CD= ![]()
【解析】(1)连接BD,OD,运用直径所对的圆周角为90°,结合直角三角形斜边中线等于斜边的一半,即可求证;(2)通过证明△BCD∽△ACB,结合三角形的中位线定理即可证明;(3)在直角三角形BDC和直角三角形ABC中,运用三角函数即可求出CD和AC的值,进而求解.

练习册系列答案
相关题目