题目内容
如图，BC为⊙O的直径，AD⊥BC，垂足为D，
=
，BF和AD相交于E．试猜想AE与BE的长度之间的关系，并请说明理由．
 |
| AB |
|
| AF |
AE=BE，理由为：
补成完整的圆延长AD到点G，
根据垂径定理可知：
=
=
，
则∠ABF=∠BAG（等弧所对的圆周角相等），
则AE=BE（等角对等边）．
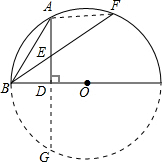
补成完整的圆延长AD到点G，
根据垂径定理可知：
|
| BG |
|
| AB |
|
| AF |
则∠ABF=∠BAG（等弧所对的圆周角相等），
则AE=BE（等角对等边）．
练习册系列答案
相关题目
，并与弧AB相交于点M、N．
