题目内容
我们知道:有两条边相等的三角形叫做等腰三角形.类似地,我们定义:至少有一组对边相等的四边形叫做等对边四边形.
(1)请写出一个你学过的特殊四边形中是等对边四边形的图形的名称;
(2)如图,在△ABC中,点D,E分别在AB,AC上,设CD,BE相交于点O,
若∠A=60°,∠DCB=∠EBC=
∠A.请你写出图中一个与∠A相等的角,并猜想图中哪个四边形是等对边四边形;
(3)在△ABC中,如果∠A是不等于60°的锐角,点D,E分别在AB,AC上,且∠DCB=∠EBC=
∠A.探究:满足上 述条件的图形中是否存在等对边四边形,并证明你的结论.
述条件的图形中是否存在等对边四边形,并证明你的结论.
(1)请写出一个你学过的特殊四边形中是等对边四边形的图形的名称;
(2)如图,在△ABC中,点D,E分别在AB,AC上,设CD,BE相交于点O,
若∠A=60°,∠DCB=∠EBC=
| 1 |
| 2 |
(3)在△ABC中,如果∠A是不等于60°的锐角,点D,E分别在AB,AC上,且∠DCB=∠EBC=
| 1 |
| 2 |
 述条件的图形中是否存在等对边四边形,并证明你的结论.
述条件的图形中是否存在等对边四边形,并证明你的结论.(1)回答正确的给(1分)(如:平行四边形、等腰梯形等).
(2)答:与∠A相等的角是∠BOD(或∠COE),
∵∠BOD=∠OBC+∠OCB=30°+30°=60°,
∴∠A=∠BOD,
猜想:四边形DBCE是等对边四边形;
(3)答:此时存在等对边四边形,是四边形DBCE.
证法一:如图,作CG⊥BE于G点,作BF⊥CD交CD延长线于F点.
∵∠DCB=∠EBC=
∠A,BC为公共边,
∴△BCF≌△CBG,
∴BF=CG,
∵∠BDF=∠ABE+∠EBC+∠DCB,∠BEC=∠ABE+∠A,
∴∠BDF=∠BEC,
∴△BDF≌△CEG,
∴BD=CE
∴四边形DBCE是等对边四边形.
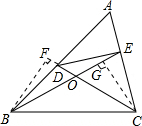
证法二:如图,以C为顶点作∠FCB=∠DBC,CF交BE于F点.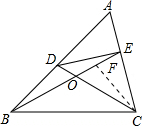
∵∠DCB=∠EBC=
∠A,BC为公共边,
∴在△BDC与△CFB中,
∴△BDC≌△CFB(ASA),
∴BD=CF,∠BDC=∠CFB,
∴∠ADC=∠CFE,
∵∠ADC=∠DCB+∠EBC+∠ABE,∠FEC=∠A+∠ABE,
∴∠ADC=∠FEC,
∴∠FEC=∠CFE,
∴CF=CE,
∴BD=CE,
∴四边形DBCE是等对边四边形.
说明:当AB=AC时,BD=CE仍成立.只有此证法,只给(1分).
(2)答:与∠A相等的角是∠BOD(或∠COE),
∵∠BOD=∠OBC+∠OCB=30°+30°=60°,
∴∠A=∠BOD,
猜想:四边形DBCE是等对边四边形;
(3)答:此时存在等对边四边形,是四边形DBCE.
证法一:如图,作CG⊥BE于G点,作BF⊥CD交CD延长线于F点.
∵∠DCB=∠EBC=
| 1 |
| 2 |
∴△BCF≌△CBG,
∴BF=CG,
∵∠BDF=∠ABE+∠EBC+∠DCB,∠BEC=∠ABE+∠A,
∴∠BDF=∠BEC,
∴△BDF≌△CEG,
∴BD=CE
∴四边形DBCE是等对边四边形.
证法二:如图,以C为顶点作∠FCB=∠DBC,CF交BE于F点.

∵∠DCB=∠EBC=
| 1 |
| 2 |
∴在△BDC与△CFB中,
|
∴△BDC≌△CFB(ASA),
∴BD=CF,∠BDC=∠CFB,
∴∠ADC=∠CFE,
∵∠ADC=∠DCB+∠EBC+∠ABE,∠FEC=∠A+∠ABE,
∴∠ADC=∠FEC,
∴∠FEC=∠CFE,
∴CF=CE,
∴BD=CE,
∴四边形DBCE是等对边四边形.
说明:当AB=AC时,BD=CE仍成立.只有此证法,只给(1分).


练习册系列答案
相关题目
 D不重合);且∠BEF=120°,设AE=x,DF=y.
D不重合);且∠BEF=120°,设AE=x,DF=y.



