题目内容
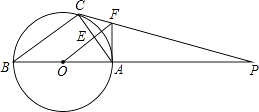
【题目】如图,已知直线y= ![]() x﹣3与x轴、y轴分别交于A、B两点,P在以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB,则△PAB面积的最大值是 .
x﹣3与x轴、y轴分别交于A、B两点,P在以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB,则△PAB面积的最大值是 . 
【答案】![]()
【解析】过C作CD⊥AB于D,延长DC交⊙C于点P′,此时△P′AB的面积最大,如图所示:
∵直线y=![]() x﹣3与x轴、y轴分别交于A、B两点,
x﹣3与x轴、y轴分别交于A、B两点,
当x=0时,y=-3;当y=0时,x=4,
∴B(0,-3),A(4,0),
∴BO=3,AO=4,
∴AB=![]() =5,
=5,
∵C(0,1),
∴BC=1-(-3)=4,
又∵∠ABO=∠DBC,∠AOB=∠CDB=90°,
∴△AOB∽△CDB,
∴![]() =
=![]() ,
,
∴CD=![]() ,
,
∵⊙C半径为1,
∴P′C=1,
∴P′D=P′C+CD=1+![]() =
=![]() ,
,
∴S△P′AB=![]() ·AB·P′D=
·AB·P′D=![]() ×5×
×5×![]() =
=![]() .
.
故答案为:![]() .
.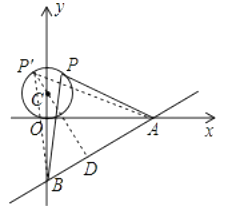
过C作CD⊥AB于D,延长DC交⊙C于点P′,此时△P′AB的面积最大;根据直线解析式得B(0,-3),A(4,0),由勾股定理得AB=5,
根据B、C坐标得BC=4,再由相似三角形判定得△AOB∽△CDB,根据相似三角形性质得![]() =
=![]() ,代入数值得CD=
,代入数值得CD=![]() ,由已知得P′C=1,
,由已知得P′C=1,
再由P′D=P′C+CD=![]() ,根据三角形面积公式得S△P′AB=
,根据三角形面积公式得S△P′AB=![]() ·AB·P′D=
·AB·P′D=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目