题目内容
【题目】如图，抛物线y=ax 
+bx+c经过点（-1,0），对称轴l如图所示．则下列结论：①
abc ＞0；②a-b+c=0；③2a+c＜0；④a+b＜0，其中所有正确的结论是（ ）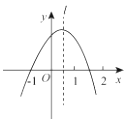
A.①③
B.②③
C.②④
D.②③④
【答案】D
【解析】①∵二次函数的图象开口向下，
∴a<0，
∵对称轴在y轴右侧，
∴
>0，
∴b>0，
∵图象与y轴的交点在y轴正半轴上，
∴c>0，
∴abc<0，
故①错误；
②∵抛物线y=ax2+bx+c经过点（-1,0），
∴a-b+c=0，
故②正确；
③∵a-b+c=0，
∴b=a+c，
根据图象，当x=2时，y<0，即4a+2b+c<0，
∴4a+2（a+c）+c<0，
化简得：2a+c＜0，
故③正确；
④∵a-b+c=0，
∴c=b-a，
根据图象，当x=2时，y<0，即4a+2b+c<0，
∴4a+2b+b-a<0，
化简得：a+b＜0，
故④正确.
综上，正确的是：②③④.
故答案为：D.
本题考查二次函数图象与系数的关系，利用二次函数性质及代数式的变形逐项判断即可.
A加金题 系列答案
全优测试卷系列答案
【题目】随着我国经济社会的发展，人民对于美好生活的追求越来越高．某社区为了了解家庭对于文化教育的消费情况，随机抽取部分家庭，对每户家庭的文化教育年消费金额进行问卷调查，根据调查结果绘制成如下两幅不完整的统计图表．
组別 | 家庭年文化教育消费金额x（元） | 户数 |
A | x≤5000 | 36 |
B | 5000＜x≤10000 | 27 |
C | 10000＜x≤15000 | m |
D | 15000＜x≤20000 | 33 |
E | x＞20000 | 30 |
请你根据统计图表提供的信息，解答下列问题：
（1）本次被调查的家庭有 户，表中m＝ ；
（2）请说明本次调查数据的中位数落在哪一组？
（3）在扇形统计图中，D组所在扇形的圆心角为多少度？
（4）这个社区有2500户家庭，请你估计年文化教育消费在10000元以上的家庭有多少户？
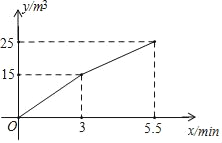
【题目】为了鼓励市民节约用水，某市水费实行分段计费制，每户每月用水量在规定用量及以下的部分收费标准相同，超出规定用量的部分收费标准相同．例如：若规定用量为10吨，每月用水量不超过10吨按1.5元/吨收费，超出10吨的部分按2元/吨收费，则某户居民一个月用水8吨，则应缴水费：8×1.5=12（元）；某户居民一个月用水13吨，则应缴水费：10×1.5+（13﹣10）×2=21（元）．
表是小明家1至4月份用水量和缴纳水费情况，根据表格提供的数据，回答：
月份 | 一 | 二 | 三 | 四 |
用水量（吨） | 6 | 7 | 12 | 15 |
水费（元） | 12 | 14 | 28 | 37 |
（1）该市规定用水量为 吨，规定用量内的收费标准是 元/吨，超过部分的收费标准是 元/吨．
（2）若小明家五月份用水20吨，则应缴水费 元．
（3）若小明家六月份应缴水费46元，则六月份他们家的用水量是多少吨？
