题目内容
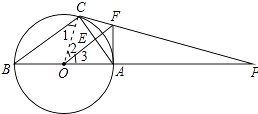
【题目】如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P.OF∥BC交AC于点E,交PC于点F,连结AF.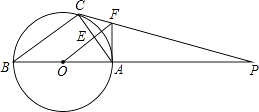
(1)判断AF与⊙O的位置关系并说明理由;
(2)已知半径为20,AF=15,求AC的长.
【答案】
(1)解:证明:连接OC,如图所示:
∵AB是⊙O直径,
∴∠BCA=90°,
∵OF∥BC,
∴∠AEO=90°,∠1=∠2,∠B=∠3,
∴OF⊥AC,
∵OC=OA,
∴∠B=∠1,
∴∠3=∠2,
在△OAF和△OCF中,
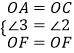 ,
,
∴△OAF≌△OCF(SAS),
∴∠OAF=∠OCF,
∵PC是⊙O的切线,
∴∠OCF=90°,
∴∠OAF=90°,
∴FA⊥OA,
∴AF是⊙O的切线;
(2)解:∵⊙O的半径为20,AF=15,∠OAF=90°,
∴OF= ![]() =
= ![]() =25
=25
∵FA⊥OA,OF⊥AC,
∴AC=2AE,△OAF的面积= ![]() AFOA=
AFOA= ![]() OFAE,
OFAE,
∴15×20=25×AE,
解得:AE=12,
∴AC=2AE=24.
【解析】(1)根据题意由AB是⊙O直径,得到∠BCA=90°,已知OF∥BC,得到∠3=∠2,根据两边对应相等且夹角对应相等的两三角形全等,得到△OAF≌△OCF,再由PC是⊙O的切线,得到AF是⊙O的切线;(2)在⊙O中由勾股定理求出OF的值,由FA⊥OA,OF⊥AC,得到△OAF的面积的代数式,求出AC=2AE的值.

 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案【题目】随着我国经济社会的发展,人民对于美好生活的追求越来越高.某社区为了了解家庭对于文化教育的消费情况,随机抽取部分家庭,对每户家庭的文化教育年消费金额进行问卷调查,根据调查结果绘制成如下两幅不完整的统计图表.
组別 | 家庭年文化教育消费金额x(元) | 户数 |
A | x≤5000 | 36 |
B | 5000<x≤10000 | 27 |
C | 10000<x≤15000 | m |
D | 15000<x≤20000 | 33 |
E | x>20000 | 30 |
请你根据统计图表提供的信息,解答下列问题:
(1)本次被调查的家庭有 户,表中m= ;
(2)请说明本次调查数据的中位数落在哪一组?
(3)在扇形统计图中,D组所在扇形的圆心角为多少度?
(4)这个社区有2500户家庭,请你估计年文化教育消费在10000元以上的家庭有多少户?