Question

【题目】如图1，抛物线y=﹣x2+2x+3与x轴相交于A，B两点（点A在点B的左侧），与y轴相交于点C．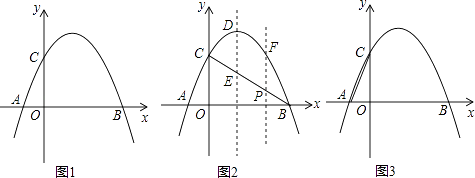

（1）直接写出A，B，C三点的坐标和抛物线的对称轴；
（2）如图2，连接BC，与抛物线的对称轴交于点E，点P位线段BC上的一个动点，过点P作PF∥DE交抛物线于点F，设点P的横坐标为m；用含m的代数式表示线段PF的长；并求出当m为何值时，四边形PEDF为平行四边形？
（3）如图3，连接AC，在x轴上是否存在点Q，使△ACQ为等腰三角形，若存在，请求出点Q的坐标，若不存在，请说明理由．

Answer 1

【答案】
（1）解：当y=0时，﹣x2+2x+3=0，解得x1=﹣1，x2=3，则A（﹣1，0），B（3，0），

当x=0时，y=﹣x2+2x+3=3，则C（0，3）；

抛物线的对称轴是直线x= =1

（2）解：设直线BC的函数关系式为y=kx+b，

把B（3，0），C（0，3）分别代入得 ，解得k=﹣1，b=3，

∴直线BC的函数关系式为y=﹣x+3，

∵对称轴是直线x=1，

∴E（1，2），

∵y=﹣x2+2x+3=﹣（x﹣1）2+4，

∴顶点D的坐标为（1，4），

当x=m 时，y=﹣m+3，

∴P（m，﹣m+3），F（m，﹣m2+2m+3），

∴线段DE=4﹣2=2，线段PF=﹣m2+2m+3﹣（﹣m+3）=﹣m2+3m；

∵PF∥DE，

∴当PF=ED时，四边形PEDF为平行四边形，即﹣m2+3m=2，解得m1=2，m2=1（不合题意，舍去），

∴当m=2时，四边形PEDF为平行四边形

（3）解：设在x轴上存在点Q（x，0），使△ACQ为等腰三角形．分三种情况：

①如果QA=QC，那么（x+1）2=x2+32，

解得x=4，

则点Q1（4，0）；

②如果CA=CQ，那么12+32=x2+32，

解得x1=1，x2=﹣1（不合题意舍去），

则点Q2（1，0）；

③如果AC=AQ，那么12+32=（x+1）2，

解得x1= ﹣1，x2=﹣ ﹣1，

则点Q3（ ﹣1，0），Q4（﹣ ﹣1，0）；

综上所述存在点Q，使△ACQ为等腰三角形．它的坐标为：Q1（4，0），Q2（1，0），Q3（ ﹣1，0），Q4（﹣ ﹣1，0）．

【解析】（1）通过解方程-x2+2x+3=0可得A点和B点坐标，再计算自变量为0时的函数值可得到C点坐标，然后利用对称性可确定抛物线的对称轴；
（2）先利用待定系数法求出直线BC的函数关系式为y=-x+3，再确定E（1，2），D（1，4），表示出P（m，-m+3），F（m，-m2+2m+3），接着计算出DE=2，PF=-m2+3m，然后利用平行四边形的判定方法得到-m2+3m=2，再解方程求出m即可．
（3）分三种情况：QA=QC；CA=CQ；AC=AQ；进行讨论即可求解．
【考点精析】利用一次函数的性质和坐标确定位置对题目进行判断即可得到答案，需要熟知一般地，一次函数y=kx+b有下列性质：（1）当k>0时，y随x的增大而增大（2）当k<0时，y随x的增大而减小；对于平面内任一点P，过P分别向x轴，y轴作垂线，垂足分别在x轴，y轴上，对应的数a,b分别叫点P的横坐标和纵坐标．